Курсовая работа: Задачи на экстремум в планиметрии

Пусть аргумент перешел через значение х ₁ = — 1, но не дошел до следующего критического значения х₂ = ¹ /₅ . Тогда двучлен х + 1 стал положителен, а два других двучлена формулы (3) остаются отрицательными, и мы имеем: f '(х ) = 5 (+)² (-)(-) = +.(5)

Сравнив (4) и (5), видим, что при переходе

Рис. 11 через критическое значение х ₁ = -1 производная не меняет знака, оставаясь положительной. Значит, в точке х =-1 экстремума нет; здесь функция f (x ) возрастает (рис. 11).

б) Исследуем ближайшее большее критическое значение х ₂ = ¹ /₅ . В достаточной близости слева (т. е. между х ₁ = — 1 и х ₂ = ¹ /₅ ) производная в силу (5) положительна. В достаточной близости справа (между х ₁ = ¹ /₅ и х₂ = +1) второй сомножитель положителен, и мы имеем:

f ' (х ) = 5 (+)² (+) (-) = - . (6)

Сравнив (5) и (6), видим, что знак производной при переходе через х₂ = ¹ /₅ меняется с плюса на минус [функция f (х ) от возрастания переходит к убыванию]. Значит, в точке x = ¹ /₅ функция имеет максимальное значение; оно равно f (¹ /₅ ) = (¹ /₅ – 1)² (¹ /₅ + 1) ~ 1,1.

в) Исследуем последнее критическое значение х₃ = 1. В достаточной близости слева производная в силу (6) отрицательна. Справа от х₃ = 1 имеем:

f '(х ) = ¹ /₅ (+)² (+) (+) = + . (7)

При переходе через х = 1 производная меняет знак с минуса на плюс [функция f (х ) переходит от убывания к возрастанию]. Значит, при х = 1 функция имеет минимальное значение; оно равно

f (х ) = (1 - 1)² (1 + 1)³ = 0.

П р и м е р 3. Найти все экстремумы функции

Р е ш е н и е. Данная функция дифференцируема при всех положительных и отрицательных значениях х , и мы имеем:

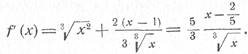
В точке же х = 0 функция f (x ) не дифференцируема (ее производная бесконечна). Поэтому (см. замечание 1) имеем два критических значения: x ₁ = 0 и х ₂ = ² /₅ .

При х < 0 имеем:

При 0 < х < ² /₅ имеем:

При х > ² /₅ имеем:

Значит, в точке х = 0 функция имеет максимальное значение f (0) = 0, а в точке x = ² /₅ - минимальное значение

§ 5. Второе достаточное условие максимума и минимума

Когда знак производной вблизи критических точек (§ 4) распознается с трудом, можно пользоваться следующим достаточным условием экстремума.

Т е о р е м а 1. Пусть в точке х = а первая производная f ' (х ) обращается в нуль; если при этом вторая производная f " (а ) отрицательна, то функция

f (х ) имеет в точке х = а максимум, если положительна, то — минимум. В случае f "(а ) = 0 см. теорему 2.

Второе условие следующим образом связано с первым. Будем рассматривать f "(х ) как производную от f '(х ). Соотношение f "(а ) < 0 означает, что f '(х ) убывает в точке х = а . Атак как f '(а ) = 0, то f (х ) положительна при х < а и отрицательна при х > а . Значит (§ 3), f (х ) имеет максимум при х = а. Аналогично для случая f " (а ) > 0.

П р и м е р 1. Найти максимумы и минимумы

Рис. 12 функции f (х ) = ½ х ⁴ – х ² + 1

Р е ш е н и е. Решив уравнение f '(х ) = 2х ³ — 2х = 0,

получаем критические значения х _l = —1, х₂ = 0, х₃ = 1.

Подставив их в выражение второй производной f "(х ) = 6х ² — 2 = 2 (Зх ² — 1), находим, что f "(-1)>0, f "(0)<0, f "(1)>0. Значит при х = -1 и х = 1 имеем минимум, при х = 0 - максимум (рис. 12).

Может случиться, что вместе с первой производной обращается в нуль и вторая; может обратиться в нуль и ряд последующих производных. Тогда можно воспользоваться следующим обобщением теоремы 1.

Т е о р е м а 2. Если в точке х = а , где первая производная равна нулю, ближайшая не равная нулю производная имеет четный порядок 2k , то функция f (х ) имеет при х = а максимум, когда f ^{(2 k )} (а ) < 0, и минимум, когда f ^{(2 k )} (а ) > 0. Если же ближайшая не равная нулю производная имеет нечетный порядок 2k + 1, то функция f (х ) в точке а не имеет экстремума; она возрастает, когда f ^{(2 k + 1)} (а ) > 0, и убывает, когда f ^{(2 k + 1)} (а ) < 0.

З а м е ч а н и е. Теоретически не исключено, что у функции f (х ) (не являющейся постоянной величиной) все производные в точке х = а будут равняться нулю. Однако практического значения этот случай не имеет.

П р и м е р 2. Найти максимумы и минимумы функции f (х ) = sin Зх - 3 sinх .