Исследуем знак разности (2) для каждой из двух критических точек Р₁ (0; 0), Р₂ (1; 1).

2а) Для точки Р₁ (0; 0) имеем:

f (x , у ) – f (0, 0) = х ³ + у ³ -Зху + 1. (5)

Разность (5) не сохраняет знака, т. е. в любой близости от Р₁ есть точки двух типов: для одних разность (5) положительна, для других — отрицательна. Так, если точку Р (х ; у ) взять на прямой у = х , то разность (5) равна

2х ³ — Зх ² = х ² (2х — 3). Вблизи от Р₁ (при х < ³ /₂ ) эта разность отрицательна. Если же точку Р (х ; у ) взять на прямой у = —х , то разность (5) равна Зх ² , а эта величина всегда положительна.

Поскольку разность (5) не сохраняет знака, в точке P₁ (0; 0) экстремума нет. Поверхность

z = х³ + у ³ — Зху + 1

в точке (0; 0; 1) имеет вид седла (наподобие гиперболического параболоида).

2б) Для точки Р₂ (1; 1) имеем:

f (x ,y ) – f (1; 1) = x ³ + y ³ - 3xy + l.(6)

Докажем, что эта разность в достаточной близости от точки (1; 1) сохраняет положительный знак. Положим:

х = 1 + α,у = 1+ β.(7)

Разность (6) преобразуется к виду

3(α ² - α β + β² ) + (α ³ + β³ )(8)

Первый член при всех ненулевых значениях α, β положителей и притом больше чем ³ /₂ (α ² + β² ). Второй член может быть и отрицательным, но при достаточной малости | α | и | β |он по абсолютному значению меньше чемα ² + β² . Значит, разность (8) положительна.

Стало быть, в точке (1; 1) данная функция имеет минимум.

§ 8.Теорема Чевы

Теорема Чевы — это классическая теорема геометрии треугольника. Эта теорема аффинная, т. е. она может быть сформулирована используя только характеристики сохраняющиеся при аффинных преобразованиях. Теорема названа в честь итальянского математика Джованни Чевы, который доказал её в 1678 году.

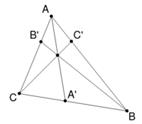
Начнём с определения: Отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне, называется чевианой .

Три чевианы AA ',BB ',CC ' треугольника конкурентны тогда и только тогда, когда

Если стороны BC, CA, ABтреугольника ABC разделены в отношениях BP/PC = λ ≠ 0, CQ/QA = µ ≠ 0, AR/ RB = υ ≠ 0, то прямые AP, BQ, CR принадлежат одному и тому же пучку (собственному или несобственному) тогда и только тогда, когда λ, µ, υ = 1.

Эту теорему можно обобщить на случай когда точки A ',B ',C ' лежат на продолжениях сторон BC ,CA ,AB . Для этого надо воспользоваться «отношением направленных отрезков», оно определено для двух направленных отрезков XY и ZT на одной прямой (или на параллельных прямых) и обозначается XY / ZT.

Пусть A ',B ',C ' лежат на прямых BC ,CA ,AB треугольника . Прямые AA ',BB ',CC ' конкурентны тогда и только тогда, когда

§9. Задачи о треугольнике наименьшего периметра, вписанного в остроугольный треугольник

Условие

Впишите в данный остроугольный треугольник ABC треугольник наименьшего периметра.

Решение

Пусть A ₁ — вершина искомого треугольника, принадлежащая стороне BC треугольника ABC . Рассмотрите образы точки A ₁ при симметриях относительно прямых AB и AC .

Пусть вершины A ₁ , B ₁ и C ₁ треугольника A ₁ B ₁ C ₁ принадлежат сторонам соответственно BC , AC и AB треугольника ABC . Рассмотрим точки M и N , симметричные точке A ₁ относительно прямых AB и AC соответственно. Тогда, если P _A1B1C1 — периметр треугольника A ₁ B ₁ C ₁ , то

P _{A 1 B 1 C 1} = A ₁ C ₁ + C ₁ B ₁ + B ₁ A ₁ = MC ₁ + C ₁ B ₁ + B ₁ N MN ,

причём равенство достигается только в случае, если прямая MN проходит через точки B ₁ и C ₁ . Поскольку AM = AA ₁ = AN , то треугольник MAN — равнобедренный и

MAN = 2BAA ₁ + 2A ₁ AC = 2BAC .