Курсовая работа: Замкнутые сети с многорежимными стратегиями обслуживания

Множители в (3.1.9) имеют форму

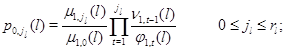
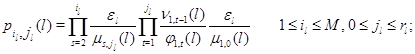
а постоянная нормировки имеет вид

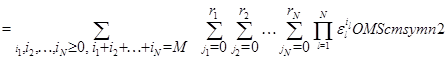
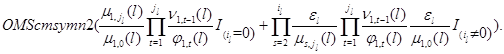
Случай . Предположим, что когда все заявок скапливаются в одном узле, прибор не может переходить с одного режима работы на другие: при . Пусть также для всех выполняется для и для , а также для и для . Это соответствует тому, что в модели из 3.1 полагается .

Следствие 2.3. Марковский процесс эргодичен. Для того, чтобы его стационарное распределение представлялось в мультипликативной форме (3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия

Множители в (3.1.9) имеют форму

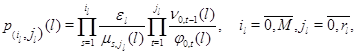
а постоянная нормировки имеет вид

Случай . Когда в узле нет заявок или все заявки скапливаются в нем, переход с одного режима работы на другие невозможен: при или . Пусть также для всех выполняется для и для , а также для и для . Это соответствует тому, что в модели из 3.1 полагается .

Следствие 2.4. Марковский процесс эргодичен. Для того, чтобы его стационарное распределение представлялось в мультипликативной форме (3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия

Множители в (3.1.9) имеют форму

а постоянная нормировки имеет вид

В следующих двух случаях стационарное распределение всегда имеет форму произведения, поскольку марковский процесс, описывающий изолированный узел в фиктивной окружающей среде, обратим. Поэтому не надо накладывать никаких ограничений типа (3.1.13), (3.1.14).