Лабораторная работа: ЭВМ с использованием математического пакета MathCad в среде Windows 98 для решения системы алгебраических уравнений

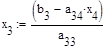
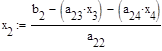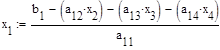
Проверим правильность нахождения корней:

Ответ: х1≈0,1 х2≈-0,67 х3≈-2,1 х4≈2,31

2.2 Решение системы линейных алгебраических уравнений методом последовательного исключения неизвестных (метод Холесского)

Метод Холесского заключается в представлении матрицы в виде произведения двух треугольных матриц L и U , имеющих следующий вид: диагональные элементы L матрицы равны единице, а элементы выше главной диагонали равны нулю; у матрицы U равны нулю элементы, лежащие ниже главной диагонали. Тогда можно записать:

,

что эквивалентно двум треугольным системам,

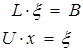
которые можно решить способом изложенным выше. Элементы l_ij , и u_ij матриц L и U можно найти, образуя произведение матриц LU и приравнивая его элементы последовательно элементам а₁₁ , а₁₁ ……. а_nn матрицы А.

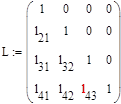
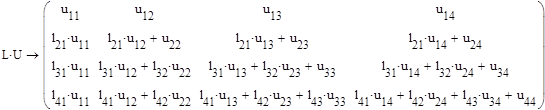
Последовательно приравниваем элементы полученной матрицы к элементам а₁₁ , а₁₁ ……. а_nn матрицы А и находим элементы l_ij , и u_ij .

По первой строке: