Лабораторная работа: Генератор случайных чисел

а) б)

Рис. 1. Графическое представление рекуррентного ГСЧ:

а) с «плохой» функцией f (x ); б) с «хорошей» функцией f (x ).

Считается, что функция f (x ) тем лучше подходит для генерирования случайных чисел, чем более плотно и равномерно ее график заполняет область x Î[0; 1], y Î[0; 1]. Например, функция, приведенная на рис. 1, а, будет давать последовательность чисел с сильной корреляционной зависимостью соседних элементов. В случае функции, приведенная на рис. 1, б, эта зависимость будет значительно слабее.

В настоящее время широкое распространение получили линейные конгруэнтные ГСЧ. В таком ГСЧ каждое следующее число получается на основе единственного предыдущего, при этом используется функция f вида:

f(х) = (ах +с ) mod m ,

где для n ‑разрядных двоичных целых чисел m обычно равно 2ⁿ .

Конгруэнтный ГСЧ выдает псевдослучайные целые числа в интервале (0, m ). Параметры x ₀ , a и c – целые числа из той же области, выбираемые исходя из следующих соображений:

1. x ₀ может быть произвольно. Для проверки программы возможно x ₀ =1. В дальнейшем в качестве x ₀ можно брать текущее время, преобразованное в число из интервала (0, m ). Такой подход обеспечивает различные последовательности для различных запусков программы.

2. Выбор a должен удовлетворять трем требованиям (для двоичных машин):

a mod 8 = 5;

;

двоичные знаки а не должны иметь очевидного шаблона.

3. В качестве c следует выбирать нечетное число, такое, что

.

Более подробные рекомендации по выбору параметров можно найти у Д. Кнута [5].

При использовании конгруэнтного ГСЧ следует помнить, что наименее значимые двоичные цифры x_k будут «не очень случайными». Поэтому, если, например, вы хотите использовать число x_k для случайного выбора одной из 16 возможных ветвей, берите наиболее значимые разряды x_k , а не наименее значимые. Наконец, для большей надежности полезно предварительно испытать случайные числа на какой-либо задаче с известным ответом, схожей с реальным приложением.

5. Генерирование чисел с произвольным распределением

Достаточно часто возникает необходимость сгенерировать последовательность случайных чисел y_i , равномерно распределенных на данном конечном интервале [a , b ], с помощью ГСЧ, выдающего числа x_i на интервале [0, m ]. Приведение диапазона ГСЧ к нужному интервалу в этом случае осуществляется простым линейным преобразованием:

.

Распределение чисел после такого преобразования остается равномерным.

Более сложным случаем является генерирование случайных точек из некоторого множества в n ‑мерном пространстве R ⁿ , например, точек из некоторой области на плоскости. Рассмотрим формирование случайных точек для нескольких простых областей: прямоугольника, окружности и круга.

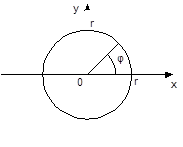
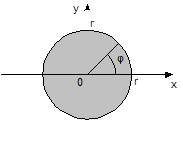
а) б) в)

Рис. 2. Области, из которых выбираются точки

Для получения равномерно распределенных случайных чисел из прямоугольника, стороны которого параллельны осям координат (см. рис.2, а), достаточно извлекать из ГСЧ последовательно пары чисел, приводить их к нужным интервалам и использовать как координаты точки:

,

где u_j – равномерно распределенное случайное число из отрезка [0, m ].