Лабораторная работа: Генератор случайных чисел

,

где P (j , l ) – вероятность появления j единиц в l разрядах числа X_i ;

p (1) = p (0) = 0,5 – вероятность появления единицы и нуля в любом разряде числа X_i ;

.

Тогда при фиксированной точке выборки N теоретически ожидаемое число появления случайных чисел X_i с j единицами в проверяемых l разрядах будет равно .

После нахождения теоретических и экспериментальных вероятностей P (j , l ) или чисел n_j при различных значениях l £ n гипотеза о стохастичности проверяется с использованием критериев согласия, которые подробно рассматриваются в курсе математической статистики.

При анализе стохастичности последовательности чисел {x_i } методом серий последовательность разбивается на элементы первого и второго рода (a и b ), т.е.

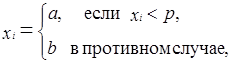
где 0 < p < 1.

Серией называется отрезок последовательности {x_i }, состоящий из идущих друг за другом элементов одного и того же рода. Число элементов в отрезке (a или b ) называется длиной серии.

После разбиения последовательности {x_i } на серии первого и второго рода будем иметь, например, серию вида

….. aabbbbaaabbbaabbab….

Так как случайные числа a и b в данной последовательности независимы и принадлежат последовательности {x_i }, равномерно распределённой на интервале (0, 1), то теоретическая вероятность появления серии длиной j в N опытах (под опытом здесь понимается генерация числа x_i и проверка условия x_i < p ) определится формулой Бернулли:

, , .

В случае экспериментальной проверки оцениваются частоты появления серий длиной j . В результате получаются экспериментальная и теоретическая зависимости P (j , l ), сходимость которых проверяется по известным критериям, причем проверку целесообразно проводить при разных значениях l и р, 0 < р < 1.

7. Генератор случайных чисел в Borland C++

В языке C, как и во многих других языках высокого уровня, существует встроенная поддержка генератора случайных чисел. Для формирования чисел используется программный ГСЧ, существующий в программе в единственном экземпляре. Таким образом, с его помощью нельзя параллельно генерировать несколько независимых случайных последовательностей без специальных ухищрений. Тем не менее, одного ГСЧ достаточно для большинства прикладных задач.

В Borland C++ (как и во многих других реализациях C/C++) используется линейный конгруэнтный ГСЧ. Длина периода этого ГСЧ составляет 2³² числа.

Для работы с ГСЧ в языке C предусмотрены следующие функции:

1) int rand()

Возвращает случайное целое число в диапазоне от 0 до RAND_MAX, где RAND_MAX – некоторая константа, зависящая от конкретной реализации ГСЧ. В Borland C++ значение RAND_MAX=32767.

2) int random (int max)

Возвращает случайное целое число в диапазоне от 0 до max‑1.

3) void srand (unsigned seed)

Устанавливает новое зерно ГСЧ. Обычно используется для установки известного начального значения x ₀ при отладке программы.

4) void randomize()

Устанавливает начальное значение, полученное из текущего системного времени путем путем преобразования его в целое число. Обычно используется для сброса ГСЧ в начале программы с целью предотвращения генерирования одних и тех же последовательностей. Не рекомендуется использовать в процессе отладки, т. к. последовательность, выбранную вызовом randomize(), сложно воспроизвести. Кроме того, не рекомендуется вызывать слишком часто или через фиксированные промежутки времени, т. к. это снизит качество («случайность») генерируемых последовательностей.

8. Практические задания

8.1 Случайные числа в заданном диапазоне