Лабораторная работа: Генератор случайных чисел

.

где u_j – равномерно распределенное случайное число из интервала (0, m ); r – радиус окружности.

В случае круга первое, что приходит в голову – воспользоваться полярной системой координат (ρ, φ ), в которой данное множество фактически представляет собой прямоугольник (а для него способ генерации чисел известен). Однако при переходе от полярных координат к декартовым нарушается распределение случайных чисел: оно становится неравномерным; плотность распределения в центре круга выше, чем по краям.

Существует несколько способов получения равномерного распределения по кругу. Рассмотрим один из них. Будем генерировать случайные пары (x, y) и для каждой из них ставить внутри круга соответствующую точку, заполняя таким образом эту область. Исходя из представлений о равномерном распределении можно предположить, что при достаточно большой длине сгенерированной последовательности на единицу площади круга будет приходиться примерно одно и то же количество точек вне зависимости от их расположения (другими словами, при равномерном распределении плотность точек по кругу будет одинакова).

Воспользуемся полярной системой координат для генерирования точек. При этом будем выбирать угол φ равномерно распределенным на интервале (0; 2π ), а распределение ρ построим следующим образом:

,

где x – равномерно распределенная на отрезке [0; 1] случайная величина. Можно показать, что при таком способе формирования координат случайные точки будут равномерно распределены по всей площади круга.

Помимо выбора из произвольного множества, часто требуется формировать числа с распределением, отличным от равномерного. Распределение обычно задается функцией плотности распределения f (x ) либо функцией распределения F (x ). Функция распределения в произвольной точке x показывает вероятность того, что случайная величина X окажется меньше данного значения x :

F (x )=P (X <x ).

Функция плотности распределения представляет собой производную F (x ):

.

Функция F (x ) для любой случайной величины является неубывающей на всем интервале (–∞; +∞), стремится к 0 при x → –∞ и к 1 при x → +∞. Для получения случайных чисел с заданным распределением F (x ) необходимо найти функцию, обратную к F (x ), т.е. такую функцию G , что для всех y =F (x ) выполняется G (y )=x . Это можно пояснить следующим образом. Предположим, что мы многократно выбираем число y, равномерно распределенное на интервале [0; 1]; каждому y мы ставим в соответствие некоторое x =G(y). Выбору 50000 игреков соответствует выбор 50000 иксов. Таким образом, доля выбранных y , лежащих между двумя фиксированными значениями, скажем y ₁ и y ₂ , в точности равна доле x , лежащих в интервале [x ₁ ; x ₂ ]. Но вероятность первого из названных событий равна | y ₂ – y ₁ |, если y распределено равномерно; следовательно, верна цепочка равенств:

доля чисел в интервале [x ₁ ; x ₂ ] = доля чисел в интервале [y ₁ ; y ₂ ] = y ₂ – y ₁ = F (x ₂ ) – F (x ₁ ) = ,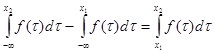

которая и показывает, что в случае равномерного распределения игреков x имеет распределение с плотностью f (τ ). Сложной проблемой в этом подходе является достаточно быстрое и точное формирование обратной функции распределения G (y ).

Рассмотрим в качестве примера получение случайного числа с экспоненциальным распределением. Это распределение характеризуется одним параметром λ>0 и имеет следующие функции распределения и плотности распределения:

, x ≥0;

.

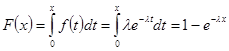Для этого распределения легко получить F ^– 1 (y ), т.е. разрешить уравнение F (x )=y . Решение имеет вид

.

Для получения x с искомым распределением нужно сгенерировать y , равномерно распределенное на (0,1), и применить эту формулу. Если говорить о практической стороне дела, то существуют более эффективные способы, в которых не используется медленная операция вычисления логарифма для каждого случайного числа. Данный способ продемонстрирован лишь как пример более общего подхода с использованием обратной функции распределения.

6. Тестирование ГСЧ

Качество ГСЧ в значительной мере влияет на результаты работы программ, использующих случайные числа. Поэтому все применяемые генераторы случайных чисел должны пройти перед моделированием системы предварительное тестирование, которое представляет собой комплекс проверок по различным стохастическим критериям, включая в качестве основных тесты на равномерность, стохастичность и независимость (рассматриваются только ГСЧ с равномерным распределением).

Проверка равномерности последовательностей псевдослучайных равномерно распределенных чисел {x_i } может быть выполнена по гистограмме с присваиванием косвенных признаков. Суть проверки по гистограмме сводится к следующему. Выдвигается гипотеза о равномерности распределения чисел (0, 1). Затем интервал (0, 1) разбивается на m равных частей, тогда при генерации последовательности {x_i } каждое из чисел x_i c вероятностью , , попадет в один из подынтервалов. Всего в каждый j ‑й подынтервал попадает N_i чисел последовательности {x_i }, , причём . Относительная частота попадания случайных чисел из последовательности {x_i } в каждый из подынтервалов будет равна N_j /N . Очевидно, что если числа x_i принадлежат псевдослучайной квазиравномерно распределенной последовательности, то при достаточно больших N экспериментальная гистограмма (ломаная линия на рис.3, а) приближается к теоретической прямой 1/m . Оценка степени приближения, т.е. равномерности последовательности {x_i }, может быть проведена с использованием критериев согласия.

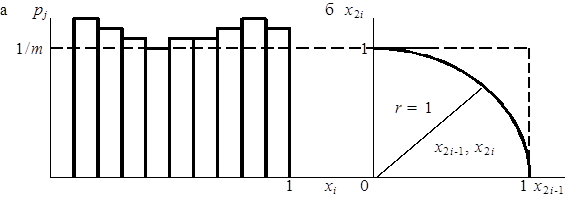
Рис. 3. Проверка равномерности последовательности

Существуют и другие способы проверки равномерности распределения.

Проверка стохастичности последовательности псевдослучайных чисел {x_i } наиболее часто проводится методами комбинаций и серий. Сущность метода сводится к определению закона распределения длин участков между единицами (нулями) или закона распределения (появления) числа единиц (нулей) в n -разрядном двоичном числе X_i .