Лабораторная работа: Интерполяция функций 2
Выполнил: ст. гр. ПМ 11 Крамарев Д. В.
Проверил: д.ф.-м.н., проф. Чехонин К.А.
Хабаровск 2004
Задание.
1) Построить интерполяционный многочлен Ньютона. Начертить график и отметить на нем узлы интерполяции. Вычислить значения в точке х=1.25.
| xi | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
| yi | 0.5 | 2.2 | 2 | 1.8 | 0.5 | 2.25 |
2) Построить интерполяционный многочлен Лагранжа. Начертить график и отметить на нем узлы интерполяции. Вычислить значение в точке х=1.2.
| xi | 0 | 0.25 | 1.25 | 2.125 | 3.25 |
| yi | 5.0 | 4.6 | 5.7 | 5.017 | 4.333 |
3)Выполнить интерполяцию сплайнами третьей степени. Построить график и отметить на нем узлы интерполяции.
| xi | 7 | 9 | 13 |
| yi | 2 | -2 | 3 |
Постановка задачи интерполяция.
Пусть известные значения функции образуют следующую таблицу:
| x0 | x1 | x2 | ... | Xn-1 | xn |
| y0 | y1 | y2 | ... | yn-1 | yn |
При этом требуется получить значение функции f в точке x, принадлежащей
отрезку [x0 ..xn ] но не совпадающей ни с одним значением xi .Часто при этом не известно аналитическое выражение функции f(x), или оно не пригодно для вычислений.
В этих случаях используется прием построения приближающей функции F(x), которая очень близка к f(x) и совпадает с ней в точках x0 , x1 , x2 ,... xn . При этом нахождение приближенной функции называется интерполяцией, а точки x0 ,x1 ,x2 ,...xn - узлами интерполяции. Обычно интерполирующую ищут в виде полинома n степени:
Pn (x)=a0 xn +a1 xn-1 +a2 xn-2 +...+an-1 x+an
Для каждого набора точек имеется только один интерполяционный многочлен, степени не больше n. Однозначно определенный многочлен может быть представлен в различных видах. Рассмотрим интерполяционный многочлен Ньютона и Лагранжа.
Интерполяционная формула Лагранжа.
Формула Лагранжа является наиболее общей, может применяться к таким узлам интерполяции, что расстояние между соседними узлами не постоянная величина.
Построим интерполяционный полином Ln (x) степени не больше n, и для которого выполняются условия Ln (xi )=yi . Запишем его в виде суммы:
Ln (x)=l0 (x)+ l1 (x)+ l2 (x)+...+ ln (x),(1)
где lk ( xi )= yi , если i=k, и lk ( xi )= 0, если i≠k;
Тогда многочлен lk ( x) имеет следующий вид:
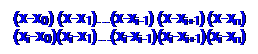lk (x)= (2)
Подставим (2) в (1) и перепишем Ln ( x) в виде:
Если функция f(x), подлежащая интерполяции, дифференцируема больше чем n+1 раз, то погрешность интерполяции оценивается следующим образом:
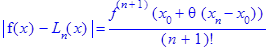
где0<θ <1 (3)
Интерполяционная формула Ньютона.
Построение интерполяционного многочлена в форме Ньютона применяется главным образом когда разность xi +1 -xi =h постоянна для всех значений x=0..n-1.
Конечная разность k-го порядка:
Δyi =yi +1 -yi
Δ2 yi = Δyi +1 - Δyi =yi +2 -2yi +1 +yi
………………………………
Δk yi =yi + k -kyi +1- k +k(k-1)/2!*yi + k-2 +...+(-1)k yi
Будем искать интерполяционный многочлен в виде:
Pn(x)=a0 +a1 (x-x0 )+a2 (x-x0 )(x-x1 )+...+an (x-x0 )(x-x1 )...(x-xn-1 )
--> ЧИТАТЬ ПОЛНОСТЬЮ <--