Кафедра: ИТ

Лабораторная работа

"ИССЛЕДОВАНИЕ ЛИНЕЙНЫХ СИСТЕМ"

Цель работы

В данной лабораторной работе средствами пакета Matlab (c использованием его расширения – пакета моделирования динамических систем Simulink) должно быть выполнено моделирование линейной системы, зафиксированы процессы, соответствующие элементам матричной весовой и переходной функций и проведено их сравнение с аналитически полученными зависимостями. Структурная схема системы представлена на рис. 1.1, коэффициенты структурной схемы - в табл. 1.1. Номер варианта для бригады указывается преподавателем.

1. Расчет матричных весовых и переходных функций

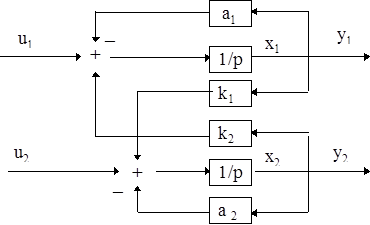
Рис. 1.1. Структурная схема системы

Таблица 1.1 Значения параметров структурной схемы

Номер варианта	1	2	3	4	5	6	7	8	9	10
a1	0,1	0,1	3	0,3	0,4	0,8	1	2	2	2
a2	0.1	0,3	0,2	0,5	0,6	1,2	3	3	4	6
k1	0,1	0,015	0,4	5	3	0,48	1,5	1	4	24
k2	0,1	2	1	0,03	0,08	2	2	6	2	0,5
Номер варианта	11	12	13	14	15	16	17	18	19	20
a1	3	0,8	0,9	0,9	0,9	1,2	3	4	4	5
a2	7	0,4	0,5	0,7	0,9	1,8	2	3	5	6
k1	0,5	0,5	2	0,12	0,5	0,1	4	2	6	4
k2	42	0,24	0,025	0,25	0,02	1,6	0,5	3	2	5

Подготовительная часть работы

Вычислить передаточную функцию (матрицу ) с использованием резольвенты матрицы динамики А:

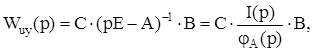
где В-матрица входов; С – матрица выходов; I(p) – присоединенная матрица для матрицы А; – характеристический полином матрицы А (I(p) и могут быть определены по методу Фаддеева-Леверье).

Найти элементы матричной весовой функции по формуле

,

где – элемент i‑й строки и j‑го столбца матричной весовой функции, интерпретируемый как реакция i‑й координаты вектора выхода на дельта-функцию в j‑й координате вектора входа .

Вычислить матричную весовую функцию по формуле

,

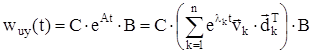где и – соответственно k‑й правый и k‑й левый собственные векторы матрицы А. Убедиться в идентичности результатов, полученных в пп. 1.2.2 – 1.2.3.

Вычислить элементы матричной переходной функции по формуле

,

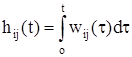где – элемент i‑й строки и j‑го столбца матричной переходной функции, интерпретируемый как реакция i‑й координаты вектора выхода на единичную функцию в j‑й координате вектора входа .

Программа работы

В ходе проведения лабораторной работы требуется в среде Matlab подготовить схему моделирования исследуемой системы, провести модельный эксперимент и зафиксировать его результаты.

Изучаемая в данной работе система описана двумя способами: при помощи структурной схемы (см. рис. 1.1) и в виде векторно-матричных уравнений, полученных в ходе подготовки к работе. Поэтому предлагается провести моделирование для двух вариантов описания системы и сравнить его результаты (процессы, соответствующие элементам матричной весовой и переходной функций) с аналитически полученными зависимостями.

Рекомендуется создать две отдельных модели: одну – для получения и фиксации 4 процессов, соответствующих элементам матричной весовой функции, вторую – для 4 процессов, соответствующих элементам матричной переходной функции.

Таким образом, должно быть зафиксировано 8 процессов, причем каждый из них будет представлен в трех вариантах, совмещенных на одном графике (т. к. моделируется система, описанная, во-первых, в виде структурной схемы и, во-вторых, – в векторно-матричной форме, а также, в-третьих, получены аналитические зависимости для и ).

Для проведения моделирования должны быть созданы 5 файлов.

1) Файл-сценарий w_h_init.m, содержащий определения всех необходимых переменных в моделях:

%Файл определениЯ переменных

--> ЧИТАТЬ ПОЛНОСТЬЮ <--