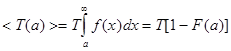Лабораторная работа: Математические модели окружающей среды

– куммулятивная частота превышения уровня а .

Рис. 3.1. Зависимость куммулятивной частоты от уровня превышения.

Разбиваем исходный ряд на на отрезков, для каждого «куска» ряда строим функции зависимости куммулятивной частоты от уровня превышения, и оцениваем стационарность полученных

n-зависимостей критериям, полученным в п. 2.

Анализируя оценки корреляционной функции, математического ожидания и дисперсии, находим период стационарности куммулятивной частоты превышения уровня T=17.85 лет.

Рис. 3.2. Оценка корреляционной функции

Рис. 3.3. Оценки математического ожидания и дисперсии.

4. С помощью пуассоновской статистики дать долгосрочный прогноз превышения уровня. На какой срок Вы гарантируете такой прогноз?

– искомая формула вероятности того, что за период времени T произойдет ровно m превышений уровня a . Вероятность возникновения таких ситуаций определяется средней частотой превышения уровня a и временем прогноза. Из анализа данных за 176 лет на стационарном периоде находим функцию зависимости средней частоты от уровня a .

Рис. 4.1. Средняя частота превышения уровня

Нас интересуют редкие события, например, превышение уровня . Соответственно, среднюю частоту превышения такого уровня можно определить из графика ,и она равна 0.0635

Зная среднюю частоту, теперь можно вычислить вероятность того, что за период, например, равный 220 лет, произойдет ровно 1,2,3,4.

Рис. 4.2. Вероятность возникновения ровно m– аварий

Зависимости вероятности от прогнозируемого времени для разного числа превышения уровня (m =1,2,3,4 ) являются немонотонными, и их максимум приходится на моменты времени

Как видно из графика, сначала более вероятным является только одно превышение уровня a = 0.6, затем два, три…

Например, вероятность того, что за 62 года произойдет три превышения уровня a =0.6, самая высокая и равна p = 0,19775.

5. Рассчитайте среднюю частоту появления выбросов и среднее время выброса

Будем рассматривать выбросы (превышение уровня, например, a =0.6) за период, на котором исходный ряд стационарен.

Выброс характеризуется следующим условием

Тогда можем найти среднюю частоту выброса за уровень а =0.6 =0.063

Средняя продолжительность выброса для стационарных случайных процессов