Лабораторная работа: Моделирование датчиков случайных чисел с заданным законом распределения

В данной цепочке равенств первое равенство следует из (3) , второе из неубывающего характера функций F( ζ) и F^-1 ( ζ) и третье из равномерного в интервале [0,1] распределения величин ζ.

Таким образом, если задана функция распределения F( y ) , то для получения случайной последовательности с таким распределением необходимо найти ее обратную функцию.

Для нахождения обратной функции можно использовать два метода: аналитический и графический .

3.Метод отбора или исключения

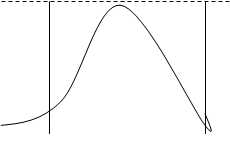
Данный метод удобнее использовать, если требуемый закон распределения задан плотностью вероятности f ( y ). В отличии от метода обратной функции метод отбора или исключения для получения одного требуемого случайного числа требует не одного равномерно- распределенного случайного числа, а двух, четырех, шести или более случайных чисел. В этом случае область возможных значений η представляет конечный отрезок ( a , b ), а плотность вероятности f ( y ) ограничена сверху значением fmax (Рис.7). Тогда область значений η^* и ζ^* можно ограничить ступенчатой кривой:

0, если y<a

g(y)= fmax, если a y b (25)

0, если y > b

Затем берутся с помощью генератора случайных чисел ( RND (ζ)) два равномерно-распределенных числа ζ_{1 и} ζ₂ , по которым определяются равномерные на интервале [ a , b ] независимые величины:

η ’ =a + (b-a)* ζ ₁

ζ ’=fmax* ζ ₂ (26)

Где a , b – границы возможных значений случайной величины η ,

fmax - максимальное значение функции f ( y ) (Рис.7)

f(y) g(y)

fmax

f(y)

ζ

a η ’ b

Рис.7 Заданная плотность вероятности

Если ζ’ f (η ’) , то η ’ принимается в качестве очередной реализации случайной величины_η . В противном случае η ’ отбрасывается и берется следующая пара равномерно- распределенных случайных чисел ζ₁ и ζ₂ . Такая процедура повторяется до тех пор, пока мы не получим требуемого количества случайных чисел с заданной плотностью вероятности.

4. Метод композиции

Метод композиции основывается на представлении плотности вероятности fη ( x ) по формуле полной вероятности:

f η ( x )=(27)

Где H ( z )= P (ζ z )– интегральная функция распределения случайной величины ζ ;

P(x / z )- условная плотность вероятности.

Переходя к дискретной форме, интеграл заменяется на сумму и тогда получаем

f η (x )=P_j *f_j (x ) (28)

где P_j =1(29)

f_j ( x ) -условная плотность вероятности