Лабораторная работа: Нахождение корня нелинейного уравнения. Методы решения системы нелинейных уравнений
Таким образом, получаем, что при выполнении условия
çg¢(C* ) ç<1(6)
последовательность (3) будет сходиться к корню с линейной скоростью a=1. Условие (6) является условием сходимости метода простой итерации. Очевидно, что успех метода зависит от того, насколько удачно выбрана функция ![]() .
.
Например, для извлечения квадратного корня, т. е. решения уравнения вида x =a2 , можно положить
x=g1 (x)=a/x (7а)
или
x=g2 (x)=(x+a/x)/2.(7б)
Нетрудно показать, что
½g1 ' (C)½=1,
½g2 ' (C)½<1.
Таким образом, первый процесс (7а) вообще не сходится, а второй (7б) сходится при любом начальном приближении С0 >0.
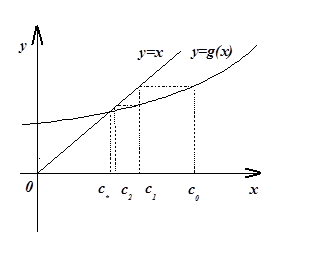
Рис. 2. Графическая интерпретация метода простых итераций для решения уравнения вида x=g(х).
Построение нескольких последовательных приближений по формуле (3)
С0 , С1 , …, Сn = C*
приведено на рисунке 2.
2.3 Метод Ньютона
В литературе этот метод часто называют методом касательных, а также методом линеаризации. Выбираем начальное приближение С0 . Допустим, что отклонение С0 от истинного значения корня С* мало, тогда, разлагая f(C* ) в ряд Тейлора в точке С0 , получим
f(C* ) = f(C0 ) + f¢(C0 ) (C* -C0 ) +¼(8)
Если f¢(C0 ) ¹ 0 , то в (8) можно ограничится линейными по DC =C-C0 членами. Учитывая, что f(C* )=0, из (9) можно найти следующее приближение для корня
C1 = C0 – f (C0 ) / f¢(C0 )
или для (n+1)-го приближения
Cn+1 = C n – f (C n ) / f ¢(C n ) (9)
Для окончания итерационного процесса можно использовать одно из двух условий
çCn +1 – Cn ç<e
или
çf(Cn +1 ) ç<e.
Исследование сходимости метода Ньютона проводится аналогично предыдущему случаю. Самостоятельно получить, что при выполнении условия
½f'' (C)/2f'(C)½<1. ![]()
![]()
метод Ньютона имеет квадратичную скорость сходимости (![]() ).
).