Лабораторная работа: принципы и методы отбора образцов проб и выборок при исследовании свойств текстильных материалов

В настоящее время при исследовании свойств текстильных материалов и других видов продукции широкое применение получили математико-статистические методы планирования экспериментов.

В задачу планирования эксперимента входят: выбор необходимых для эксперимента опытов, т.е. построение матрицы планирования, выбор методов математической обработки результатов эксперимента.

Существует два вида планирования активного эксперимента: традиционное (классическое) однофакторное и многофакторное (факторное).

В традиционном однофакторном планировании изучается влияние на выходной параметр одного входного параметра (фактора).

В результате обработки экспериментальных данных определяют взаимосвязь между выходным параметром (Y) и варьируемым на нескольких уровнях фактором (X). Математическая модель в общем виде описывается функцией отклика:

y = f ( x ) (1)

При существовании линейной связи между входными и выходными параметрами уравнение регрессии имеет следующий вид:

y = d_o +d₁ (x-x̃), (2)

где d₀ ,d₁ – коэффициенты уравнения регрессии.

Адекватность уравнения регрессии проверяется по критерию Фишера [1,4]. Если расчетное значение критерия Фишера (F_p ) меньше табличного (F_m ), то гипотеза об адекватности линейной модели не отвергается.

Выполнение работы

1. Статистическая обработка первичных результатов эксперимента

Полученные значения статистических характеристик заносим в соответствующие графы табл. 1.

Таблица 1

Расчёты статистических характеристик

№ опыта	Фактор Х	Значение параметра,Y		Ỹ	S2	S	Св
		1	2
1. 1	4	9.93	9.47	9.70	0.106	0.325	3.353
2. 2	12	9.81	9.32	9.56	0.120	0.346	3.622
3. 3	20	9.76	9.21	9.48	0.151	0.389	4.1
4. 4	27	9.74	9.16	9.45	0.168	0.41	4.34
5.	35	9.73	9.12	9.42	0.186	0.431	4.577
6.	43	9.68	9.10	9.39	0.168	0.41	4.368
7.	50	9.67	9.07	9.37	0.180	0.424	4.528
8.	58	9.64	9.04	9.34	0.180	0.424	4.542
9.	66	9.63	9.01	9.32	0.192	0.438	4.704
10.	73	9.62	9.00	9.32	0.192	0.438	4.709
11.	81	9.61	8.99	9.30	0.192	0.438	4.714
12.	88	9.62	8.97	9.29	0.212	0.46	4.945
13.	96	9.60	8.95	9.27	0.212	0.46	4.955
14.	104	9.58	8.94	9.26	0.205	0.453	4.887
15.	111	9.57	8.92	9.24	0.212	0.46	4.972
16.	119	9.54	8.92	9.23	0.192	0.438	4.75
17.	126	9.55	8.93	9.22	0.192	0.438	4.745
18.	134	9.53	8.90	9.21	0.198	0.445	4.834
19.	141	9.53	8.89	9.21	0.205	0.453	4.914
20.	149	9.52	8.88	9.20	0.205	0.453	4.919
21.	156	9.51	8.86	9.18	0.212	0.46	5.004
22.	164	9.49	8.88	9.18	0.186	0.431	4.696
23.	171	9.49	8.85	9.17	0.205	0.453	4.935
24.	179	9.49	8.82	9.15	0.225	0.474	5.175
25.	186	9.47	8.82	9.14	0.212	0.46	5.026
26.	194	9.46	8.82	9.14	0.205	0.453	4.951
27.	201	9.45	8.82	9.13	0.225	0.474	5.175
28.	209	9.47	8.80	9.13	0.212	0.46	5.026
29.	216	9.46	8.80	9.13	0.218	0.467	5.112
30.	224	9.45	8.79	9.12	0.218	0.467	5.117

2. Расчёт критерия Кочрена и проверка однородности дисперсии в опытах матрицы

Для проверки однородности дисперсии и воспроизводимости эксперимента при одинаковой повторности (m) всех опытов рассчитываем значение критерия Кочрена G_p по формуле

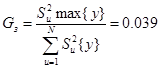(3)

где - максимальная дисперсия из всех опытов;

- сумма всех дисперсий эксперимента.

Далее расчётное значение G_p сравниваем с табличным значением G_T . Дисперсии однородны и число повторных опытов одинаково, т.к. G_p < G_T (0.039<0.3632).

3. Определение средней дисперсии выходного параметра в опытах матрицы

Т.к. в опытах матрицы дисперсии однородны и число повторных опытов одинаково, то среднюю дисперсию определяют по формуле

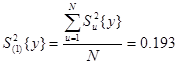(4)

После этого определяем число степеней свободы средней дисперсии;

F(S² ₍₁₎ {y})=N(m-1)=30 (5)

Средняя дисперсия характеризует средний разброс значений выходного параметра относительно его средних значений, т.е. ошибку опытов в эксперименте.

4. Определение коэффициентов регрессии и составление уравнения регрессии

Дисперсии выходного параметра для каждого уровня фактора однородны, следлвательно, применяем метод наименьших квадратов.