Лабораторная работа: Расчет характеристик и переходных процессов в электрических цепях

1. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИЧЕСКОГО СОПРОТИВЛЕНИЯ Z(w)

Для определения характеристического сопротивления нужно составить уравнение:

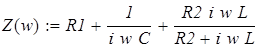
Приобразуем его:

,

.

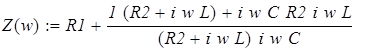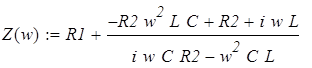
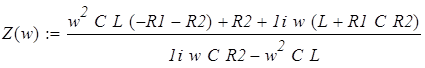Найдём модуль характеристического сопротивления ôZ(w)ô:

.

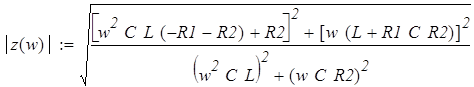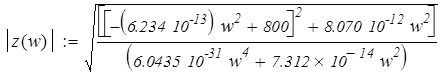
Подставив числовые значения, получим:

График зависимости модуля характеристического сопротивления от частоты показан на рисунке 1.1. Результаты расчетов представлены в дополнении А.

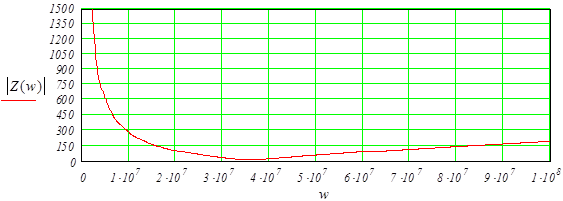
Рисунок 1.1 – График зависимости модуля характеристического сопротивления от частоты

Рассмотрим поближе тот промежуток зависимости модуля характеристического сопротивления от частоты, где он приближается к минимуму (рисунок 1.2).

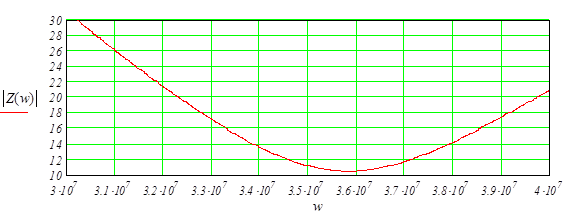
Рисунок 1.2 – График зависимости модуля характеристического сопротивления от частоты (точка минимума)

Как видно из результатов расчетов, представленных в дополнении А, минимальное значение модуля характеристического сопротивления находится на частоте 3,58 ×10⁷ рад/с.

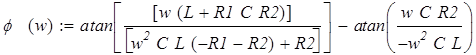
Найдём фазочастотную характеристику. Она равняется arctg от соотношения нериальной части к реальной характеристического сопротивления:

Подставив числовые значения, получим:

График ФЧХ представлен на рисунке 1.3.

Рисунок 1.3 – График фазо - частотной характеристики

2. ОПРЕДЕЛЕНИЕ КЛАССИЧЕСКИМ МЕТОДОМ ПЕРЕХОДНОЙ ХАРАКТЕРИСТИКИ , ПОСТРОЕНИЕ ГРАФИКА

Поскольку схема содержит два накопительных элемента (C и L) в различных ветвях, данная цепь является цепью второго порядка. В ней возможны либо апериодический, либо колебательный режим. Для выяснения этого составим характеристическое уравнение и определим его корни.

Для определения корней характеристического уравнения можно воспользоваться следующей методикой – записать входное сопротивление в операторной форме и приравнять его к нулю. В данной задаче получаем:

(1.1)

откуда, находим корни этого уравнения.