Научная работа: Математическая модель процесса вытяжки трубчатой заготовки
Вектор перемещений узловых точек конечного элемента в случае осесимметричной деформации имеет вид:
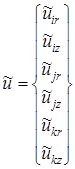 .(8)
.(8)
Произвольная точка элемента получает перемещения ur и uz в направлении осей r и z . Поэтому матрица u имеет вид:
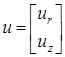 .(9)
.(9)
Узловые перемещения ![]() и u связаны между собой матрицей аппроксимирующих функций N :
и u связаны между собой матрицей аппроксимирующих функций N :
![]() (9’)
(9’)
Наиболее распространен способ получения приближённых решений на основе использования вариационного уравнения по методу Релея - Ритца. Он заключается в том, что функции перемещений задаются в виде интерполяционного полинома. Если ограничиться полиномом первой степени, то эти функции будут иметь вид:
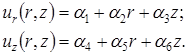 (10)
(10)
Здесь ai - произвольные постоянные. При линейной аппроксимации стороны треугольника после деформирования элемента остаются прямыми.
Выразим ai через перемещения узлов элемента. В результате матрица N примет вид:
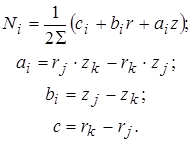 (11)
(11)
S - площадь сечения элемента:
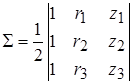 ,(12)
,(12)
где ri , zi - координаты i -го узла в соответствующих осях.
Деформированное состояние в любой точке тела описывается тензором малых деформации Коши:
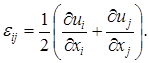 (13)
(13)
В условиях осесимметричной задачи тензор деформации второго ранга сводится к вектору:
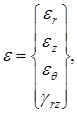 (14)
(14)
компоненты которого выражаются через производные перемещений по соответствующим координатам:
![]() .(15)
.(15)
Связь между составляющими векторов деформации и перемещений можно представить одним матричным равенством:
![]() (16)
(16)
где B – матричный дифференциальный оператор:
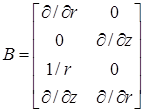 .(17)
.(17)
Используя (16) и (17), можно выразить деформации через узловые перемещения
![]() .(18)
.(18)
Матрица функций формы C для осесимметричной деформации:
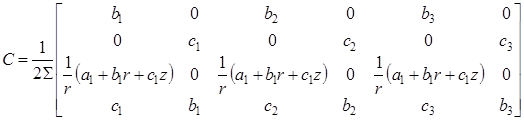 .(19)
.(19)
Коэффициенты матрицы C зависят от координат r и z точки внутри элемента. Для треугольника с узлами в вершинах координаты r и z можно заменить средними по элементу значениями: