Научная работа: Математическая модель процесса вытяжки трубчатой заготовки

Вектор напряжений s имеет вид:

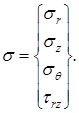(21)

Выразим с помощью линейного закона, выражаемого матрицей жёсткости, напряжения через узловые перемещения

,(21’)

где D – матрица материальных констант.

Потенциальная энергия деформации элемента с учётом (20) и (19)

.(22)

Интеграл в выражении (2.22) есть матрица жёсткости выбранного элемента

,(23)

Элементарный объём . Поэтому матрица жёсткости элемента записывается следующим образом:

,(24)

где S – площадь элемента.

С учётом проделанных преобразований уравнение равновесия элемента через узловые перемещения выражается в форме:

(25)

где K - матрица жёсткости; P , - векторы внешних сил и узловых перемещений, соответственно.

При наличии упругих и пластических деформации связь между напряжениями и деформациями нелинейна. Решение нелинейной системы уравнений весьма трудоемко. Поэтому при использовании деформационной теории часто используют кусочно-линейный закон связи напряжений и деформации. Тогда при решении задачи в приращениях напряжений D s и деформации D e , связь между которыми можно считать линейной, получаем систему линейных уравнений:

(26)

Одним из способов решения задачи в приращениях является метод последовательных нагружений. Для квазистатической задачи приращения внешних сил DP вычисляются на шаге по времени Dt . При этом вектор внешних сил P в момент времени t равен:

(27)

где n – шаг нагружения.

Таким образом, с учётом вышеизложённого, вариационное уравнение равновесия в матричной записи принимает вид:

(28)

где - вектор приращений перемещений.

3. Представление матрицы жёсткости

В пределах упругости связь между приращениями напряжений и деформации выражается законом Гука. Согласно ему компоненты приращений деформации являются линейными функциями приращений напряжений. Пластическое состояние материала описывается теорией малых упругопластических деформации Ильюшина. Принимается теория изотропного упрочнения. Объёмная деформация в пластической зоне остается упругой и для нее выполняется объёмный закон Гука:

,(29)

где q - относительное изменение объёма.

Модуль объёмного сжатия k для изотропного тела в случае осесимметричной деформации имеет вид:

.(30)

Модуль сдвига G связан с модулем Юнга E и коэффициентом Пуассона n формулой: