Реферат: Адаптивное параметрическое оценивание квадратно-корневыми информационными алгоритмами

где вектор наблюдения , матрица наблюдений , и - шум: .

Пусть также, матрицы и являются функциями неизвестного векторного параметра .

Оценкой максимального правдоподобия является такое значение оцениваемых параметров , которое максимизирует вероятность события, при котором наблюдения, сгенерированные с подстановкой оцениваемых параметров, совпадают с действительными значениями наблюдений . Эта процедура эквивалентна минимизации обратного логарифма функции плотности условной вероятности, т.е. обратный логарифм функции правдоподобия представляется как:

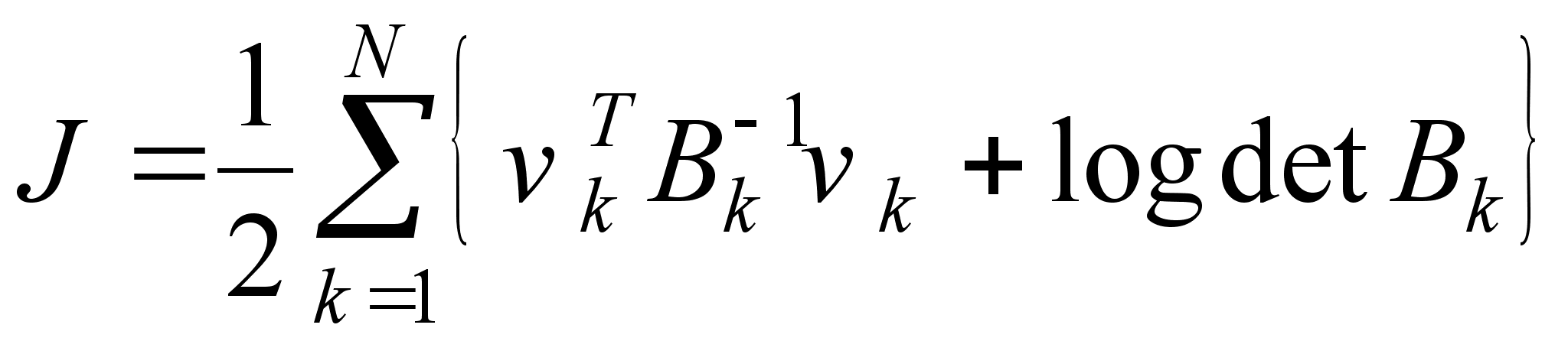(2.1.3)

где и - вычисляются согласно схеме фильтра Калмана следующим образом:

(2.1.4)

где есть ковариационная матрица ошибки экстраполяционной оценки.

Запишем другие характеристики фильтра Калмана, которые нам понадобятся в дальнейшем:

Матрица Калмана:

(2.1.5)

Матрица ковариаций измененной по последним данным ошибки:

(2.1.6)

Невязка:

(2.1.7)

Измененная оценка:

(2.1.8)

Вычисление оценки максимального правдоподобия может быть осуществлено итеративно по следующей формуле:

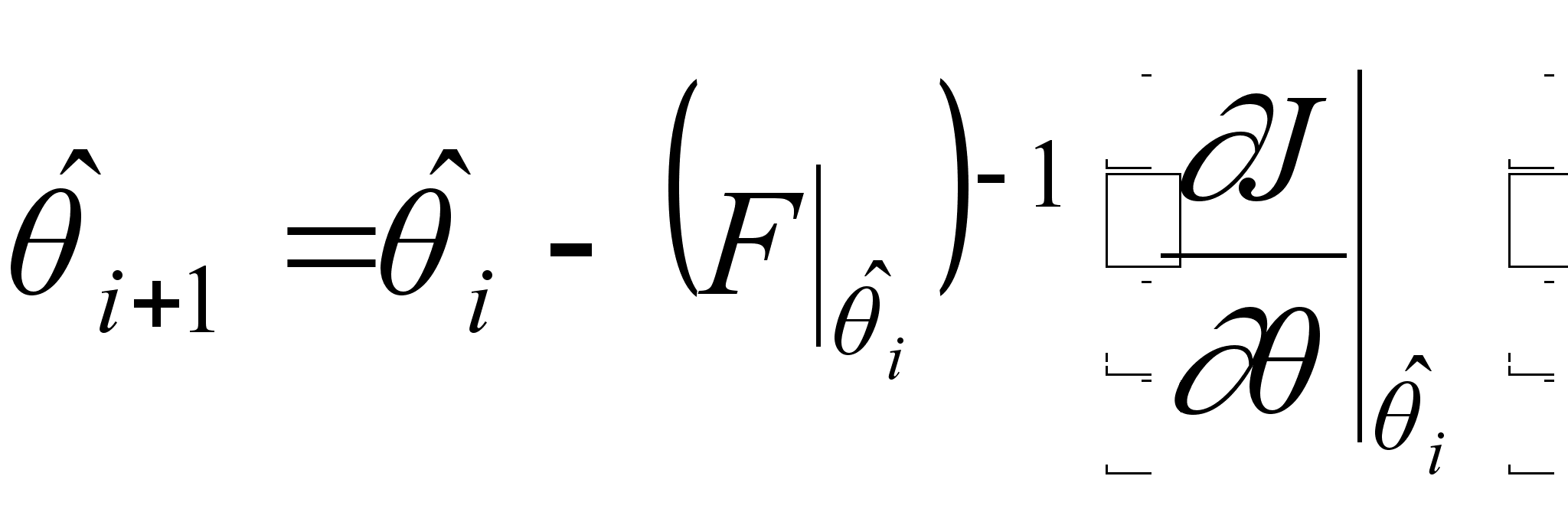(2.1.9)

где - оцениваемый векторный параметр; - индекс, определяющий номер итерации; - информационная матрица Фишера; - градиент обратного логарифма функции максимального правдоподобия.

Стоит заметить, что итеративные алгоритмы, подобные (2.1.9), в среднем сходятся за меньшее число шагов, чем те алгоритмы, которые включают в себя только вычисления . С другой стороны, алгоритмы, содержащие и , требуют больше вычислений на каждом шаге.

Модель наблюдений, в случае ККИФ, выглядит следующим образом:

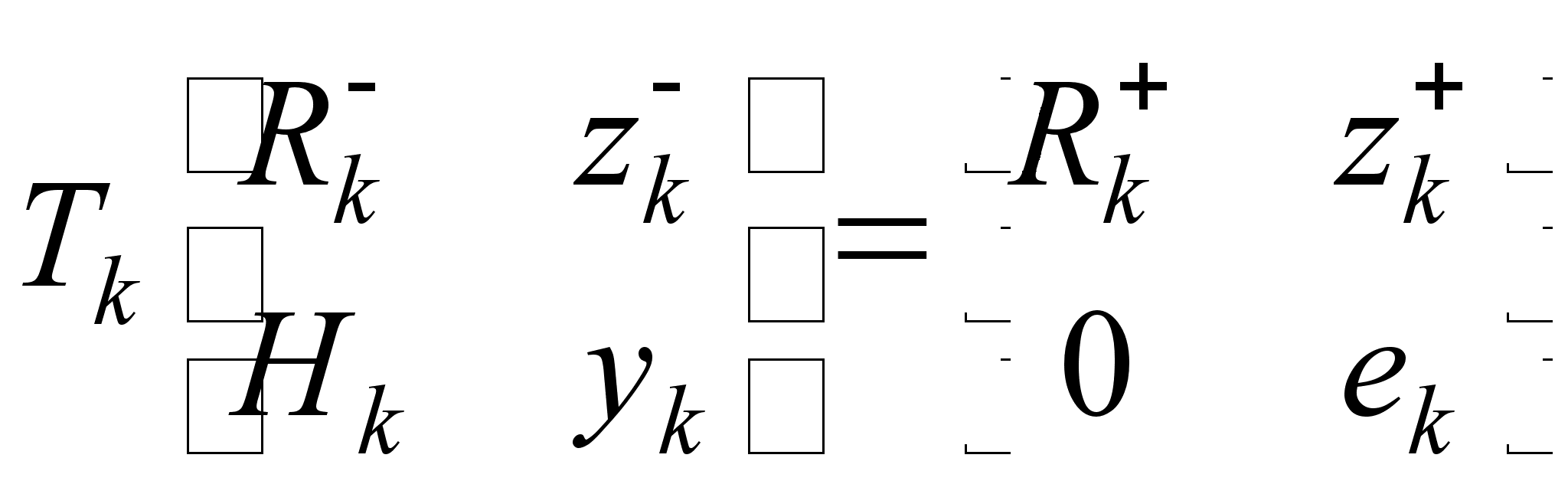(2.1.10)

где - ортогональная матрица такая, что - верхнетреугольная. Также, согласно (2.1.2) имеют вид:

(2.1.11)

где

(2.1.12)

тогда шум наблюдения имеет единичную ковариацию, что удовлетворяет ККИФ.

Шаг предсказывания ККИФ, описывается следующим образом:

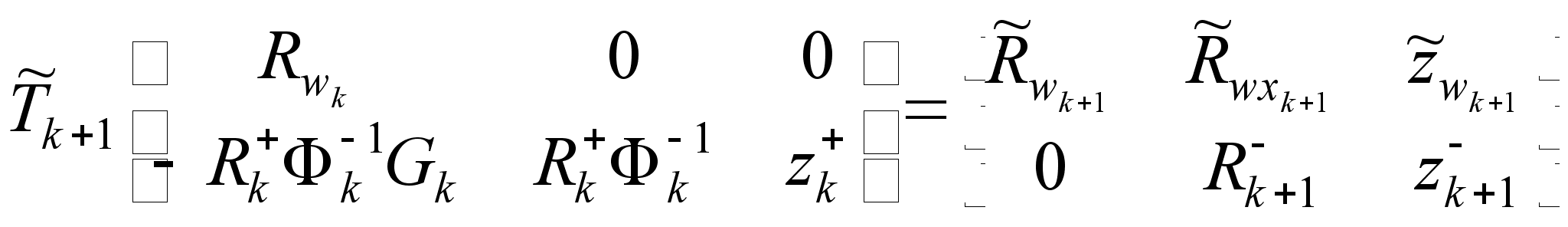(2.1.13)