Реферат: Адаптивное параметрическое оценивание квадратно-корневыми информационными алгоритмами

Таким образом:

(2.3.1)

Между тем, матрица - верхнетреугольная и должна равняться , где - верхнетреугольная часть матрицы на левой стороне (2.3.1) и - диагональная часть. И тогда, находится с помощью метода обратной подстановки решения треугольных систем.

Подводя итог выше сказанному, имеем, что градиент обратного логарифма функции максимального правдоподобия приобретает вид:

,

где все входящие величины являются либо входными значениями КИИФ, либо легко находятся путем решения треугольных систем.

Для выражения информационной матрицы Фишера в терминах ККИФ, вспомним, что - ый элемент матрицы Фишера записывается как:

Т.к. - случайный процесс с нулевым средним, то

(2.3.2)

где - -ая величина во временной последовательности, представляющей . Переписывая (2.3.2), используя ККИФ-форму представления , имеем, что - ый элемент матрицы Фишера приобретает вид:

Эта формула может быть использована и при замене ожидаемых значений переменных и вычисленными.

2.4. Значения производных переменных ККИФ

Теперь дадим численно эффективный и точный метод для вычисления значений, , которые необходимы в формулах раздела 2.3.

Для упрощения понимания положим, что преобразования ККИФ (2.1.10) и (2.1.13) имеют вид:

(2.4.1)

где - прямоугольная матрица, - ортогональная, которая при умножении с дает верхнюю трапециевидную матрицу . Элементы матрицы дифференцируемые функции параметра . Тогда, при заданных значениях производных 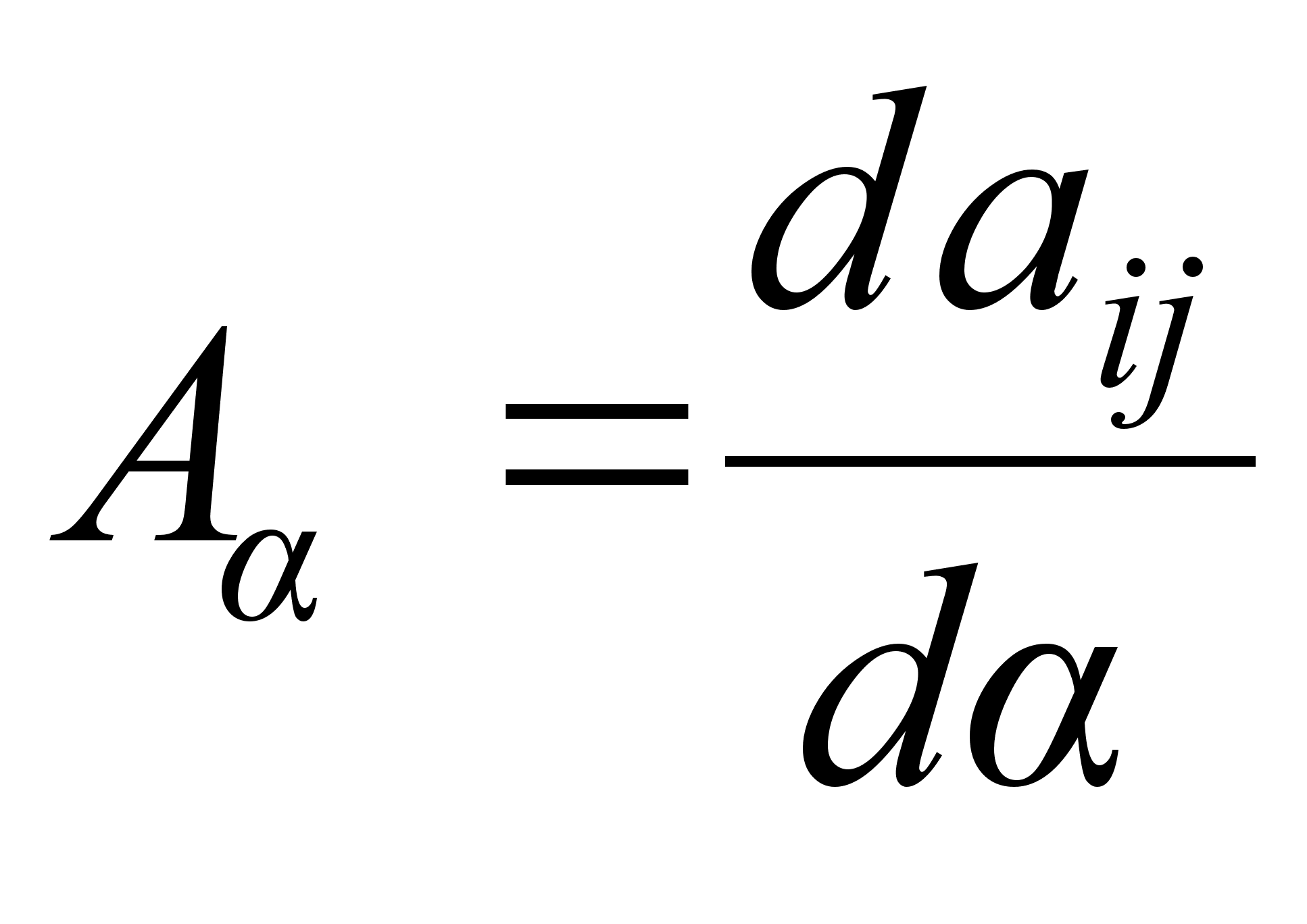, мы хотим определить матрицу .