Реферат: Алгебраическое и графическое решение уравнений, содержащих модули

значений модуля

Теперь можно рассуждать также, как и в примере 1, когда в правой части равенства находилось положительной число. Получим две смешанных системы:

(1) 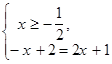и (2)

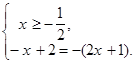
Решим каждую систему:

(1) 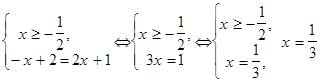входит в промежуток и является корнем уравнения.

(2) 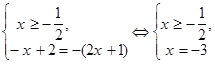x = -3 не входит в промежуток и не является корнем уравнения.

Ответ:

2-й способ

Установим, при каких значениях x модуль в левой части уравнения обращается в нуль:

Получим два промежутка, на каждом из которых решим данное уравнение (см. рис. 12):

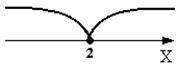
Рис. 12

В результате будем иметь совокупность смешанных систем:

Решая полученные системы, находим:

(1) входит в промежуток и является корнем уравнения.

(2) не входит в промежуток и x=-3 не является корнем уравнения

Ответ:

4.1.Решение при помощи зависимостей между числами a и b, их модулями и квадратами этих чисел.

Помимо приведенных мною выше способов существует определенная равносильность, между числами и модулями данных чисел, а также между квадратами и модулями данных чисел:

|a|=|b|  a=b или a=-b

a2=b2  a=b или a=-b (1)

Отсюда в свою очередь получим, что

|a|=|b|  a2=b2

(2)

Пример 4. Решим уравнение |x + 1|=|2x – 5| двумя различными способами.

1.Учитывая соотношение (1), получим:

x + 1=2x – 5 или x + 1=-2x + 5

x – 2x=-5 – 1 x + 2x=5 – 1

-x=-6|(:1) 3x=4