Реферат: Алгебраическое и графическое решение уравнений, содержащих модули

3)

4)

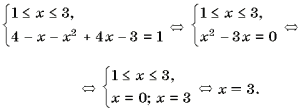
4)

Ответ: 3.

Графический способ.

Построим графики функций y = |(x–1)(x–3)| и y=1–|x–4 |

1)в Гy = |(x–1)(x–3)| подставим значение х=1 и х=3. Мы получим у=0,

тоесть пересечение графика с осью ОХ. При х равном нулю у=3, тоесть график пересекается с осью ОУ в точке (0 ;3). И при х=4 у также равен 3- мы получили первый график.

2) y=1–|x–4 | Найдем пересечение с осью ОХ, для этого решим простое уравнение: 1-|x-4|=0

|x-4|=1

x - 4=1 или x - 4=-1

x=5 x=3

Следовательно данный график пересекает ось ОХ в точках 5 и 3.

При х=4 у=1 и ак видно из графика: графики обеих функций пересекаются в одной точке 3

Ответ: 3

Пример11. Решить уравнение | x2 + 3x | = 2(x + 1).

Решение.

Уравнение равносильно системе

Ответ:

Пример12.Решить уравнение х2 - 4х +|x - 3| +3=0

Для освобождения от знака абсолютной величины разобьем числовую прямую на две области и будем искать решения исходного уравнения в каждой из этих областей отдельно:

__________x 3__________________|____________x<3_________________

|x – 3|=x – 3 |x – 3|=-x + 3

x2 - 4x + x – 3 + 3=0 x2 – 4x – x + 3 + 3=0

x2 – 3x=0 x2 – 5x + 6=0

x(x – 3)

x1=0 или x2=3 D=25 – 4  6=1> 0два различ. корня