Реферат: Алгоритмы вывода кинетических уравнений для стационарных и квазистационарных процессов

где Di = , DM = D

Из (50) и (52) получаем также

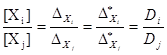(53)

В случае некаталитических реакций концентрация Xi запишется через концентрацию нуль-вещества в нуль-вершине графа

(54)

Если все [Xi] в каталитической реакции выразить через [М], получим выражение для суммарной концентрации катализатора

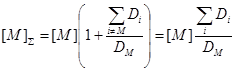(55)

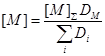(56)

Из (52) и (56) получаем

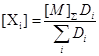(57)

В гетерогенных процессах при нормировке всех Xi к [Х]S (выражение [Xi] через доли поверхности ) получаем

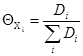(58)

Есть два способа учесть наличие висячих вершин в материальном балансе по катализатору. Найдя корневые определители для висячих вершин, их следует включить в , тогда [М]S будет включать и соединения, находящиеся в висячих вершинах. Поскольку ребра графа, инцидентные висячим вершинам, в случае стационарных и квазистационарных процессов являются равновесными стадиями, можно ввести дополнительную функцию – закомплексованность интермедиата (любой вершины циклического графа)

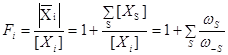(59)

где [XS] – концентрация соединения в висячей вершине графа, связанной с графом стадией S, wS и w–S – веса стадии, инцидентной висячей вершине и направленной от Xi к XS. Очевидно, что отношение включает константу равновесия KS и концентрации участников реакции, входящие в wS и w–S. Так, для вершины М в графе КГ4 получим

Формула (57) может быть модифицирована, поскольку ,

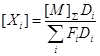(60)

По уравнению стационарности стадий легко установить связь скорости стадии со скоростью по маршруту, и таким образом найти R_P . При отсутствии висячих вершин F_i = 1.

Другой алгоритм был предложен Волькенштейном и Гольдштейном и модифицирован Яблонским и сотрудниками. На графе многомаршрутной реакции выбирается стадия, принадлежащая одному из маршрутов (W_j = R_P ), и скорость этой стадии записывается уравнением (64)

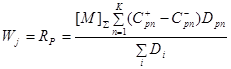, (64)

(или через SF_i D_i для случая с висячими вершинами)

где – вес n-ого цикла по маршруту Р, включающего стадию j, D_pn – определитель подграфа, получающегося при сжатии n-ого цикла по маршруту Р в одну вершину с корнем в полученной при сжатии вершине, К – число циклов, проходящих через стадию j.

Если скорость по маршруту Р описывается комбинацией скоростей стадий W_j , то уравнение (64) записывается для всех стадий.

Пример 8. Рассмотрим КГ5. Из графа видно, что базис маршрутов включает два маршрута (два простых цикла). Выберем эти простые циклы в качестве базиса. Первый маршрут включает стадии 1 и 2, второй – 1, 3, 4. Из КГ5 с очевидностью следует, что W₂ = R₁ и W₄ = R₂ . Естественно, что и W₃ = R₂ , но для упрощения вывода возьмем необратимую стадию 4. По второму алгоритму запишем величины циклов С_pn .

;

(= 0);