Реферат: Алгоритмы вывода кинетических уравнений для стационарных и квазистационарных процессов

;

; .

Запишем величины подграфов D_pn : D₁₁ = w_–3 + w₄ (сумма весов деревьев, входящих в вершину, полученную при сжатии цикла 11), D₁₂ = 1 (одной вершине соответствует D_pn = 1), D₂₁ = 1 и D₂₂ = 1. Используя величины D_M , и , найденные выше, запишем выражения для R₁ и R₂ :

(64)

(65)

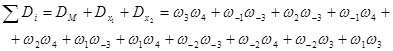
Для одномаршрутной реакции скорость стадии , а в случае линейного механизма n_S = 1. Следовательно

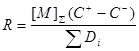(66)

Полезно отметить, что в этом случае циклическая характеристика С = С⁺ – С^– соответствует закону действия масс, записанному для итогового уравнения одномаршрутной реакции как элементарной стадии.

Пример 9.

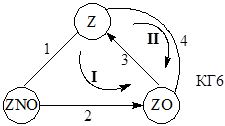
Механизм реакции изобразим КГ6:

(1)

(2)

(3)

(4)

Стехиометрический анализ механизма привел к матрице Г для Р = 2 с соответствующим набором независимых итоговых уравнений (Q_P = 2)

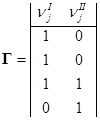
I)

II)

На КГ6 указаны эти маршруты, соответствующие двум минимальным циклам КГ6. При сложении двух векторов получим маршрут N^{II *} (1 1 2 1) с уравнением 2NO + 2CO®N₂ + 2CO₂ , а при вычитании – маршрут N^{II **} (1 1 0 –1), включающий цикл из 1, 2 и 4 стадий: 2NO + N₂ ® 2N₂ O. Из условия стационарности стадий () и КГ6 следует, что

W₁ = R₁ , W₂ = R₁ , W₃ = R₁ + R₂ , W₄ = R₂

(для маршрутов I и II)

Используем алгоритмы Яблонского (64) и Мезона (62). Для обоих уравнений нужны величины D_i . Запишем для каждой вершины i произведения сумм весов стадий, выходящих из всех других вершин КГ j¹i. Перемножим скобки и исключим из полученных сумм произведения стадий, образующих цикл, включая произведения . В результате получим D_i . Для графа КГ6 запишем произведения сумм весов стадий:

Здесь нет циклов и .