Реферат: Аналитическая теория чисел. L-функция Дирихле
справедлива также при Res<l/2; кроме того ξ(0, χ)≠ 0. Поскольку In Г(s) ~ slnsпри s-> +∞, по теореме 5.3 получаем первое утверждение теоремы. Так как L(s, χ)≠0 при Res>l, то из
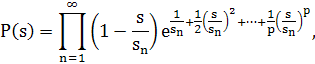
следует, что ξ(s, χ) ≠0 при Res < 0, т. о. нули ξ(s, χ) являются нетривиальными нулями L(s, χ),лежащими в полосе 0≤Res≤l. Теорема доказана.
§6. Обобщенная гипотеза Римана
Функция ζ(s) определена для всех комплексных s≠1 , и имеет нули для отрицательных целых s = —2, —4, —6 .... Из функционального уравнения
![]() ,
,
и явного выражения
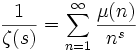
при Res >1 следует, что все остальные нули, т.е. нетривиальные, расположены в полосе 0≤Res ≤ 1 симметрично относительно критической линии ![]() . Гипотеза Римана утверждает, что:
. Гипотеза Римана утверждает, что:
Все нетривиальные нули дзета-функции имеют действительную часть, равную ![]() .
.
Обобщённая гипотеза Римана состоит из того же самого утверждения для обобщений дзета-функций, то есть L-функций Дирихле
Библиографический список
1. А.Л. Карацуба, Основы аналитической теории чисел // 2-е над.— М.: Наука. Главная редакция физико-математической литературы, 1983. -240 с.
2. С.М. Воронин, А.А. Карацуба, Дзета-функция Римана // М.: Физматлит. 1994. -376с.