Реферат: Аналіз перетворень сігналів

Таблиця 1 – Зв’язок між мінімальною відстанню та енергією сигналу на біт

Метод модуляції	ФМ-4	ФМ-8	АФМ-8	КАМ-16
d	2	1,326	1,549	1,265

Необхідно навести сигнальне сузір’я для заданого методу модуляції, пронумерувати сигнальні точки s ₀ , s ₁ , …, s_{M –1} , визначити координати сигнальних точок та занести їх до таблиці на зразок таблиці 2. Для визначення координат сигнальних точок слід визначити

Е _б = Р_s Т _б , (4.9)

де Р_s – середня потужність сигналу (задана в завданні на КР). Потім визначити d за співвідношенням з табл. 1 і всі координати сигнальних точок, враховуючи геометричну структуру сузір’я.

Таблиця 2 – Опис сигнального сузір’я та маніпуляційний код

si	ai	bi	Кодова комбінація
s0 s1	0,345 0,115	0,115 0,115	1101 1100

Відповідність між сигналами s_i та кодовими комбінаціями визначає маніпуляційний код [5, розд. 2.2]. Довжина маніпуляційного коду визначається співвідношенням (4.7). Кращий маніпуляційний код – це код Грея. У разі коду Грея кодові комбінації, що відповідають будь-яким двом найближчим сигналам, відрізняються лише в одному розряді.

Рекомендується на закінчення цього розділу виконати розрахунки, що підтверджують зв’язок між d та E _б , який наведений у табл. 1.

5 РозрахункИ частотних та часових характеристик сигналів,

що передаються каналОм зв’язку

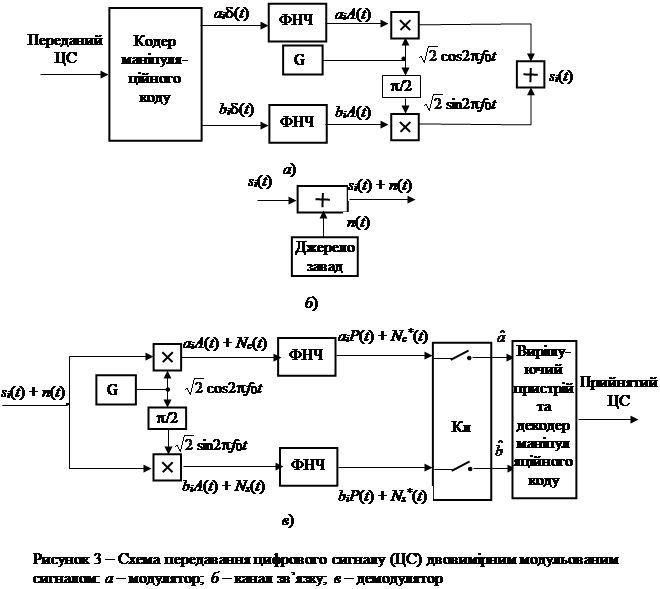
Поданий у розділі 4 опис двовимірних модульованих сигналів визначає схеми модулятора та демодулятора, які разом з моделлю каналу зв’язку наведені на рис. 3.

Позначення на рис. 3 відносяться до деякого тактового інтервалу. Кодер маніпуляційного коду на основі n = log₂ M біт (n біт можуть створити М різних кодових комбінацій) виробляє координати і -го сигналу a_i і b_i (одного з М можливих сигналів). Ці числа кодер видає на своїх виходах у вигляді двох коротких імпульсів амплітуди a_i і b_i – математично імпульси описуються як a _i d(t ) і b_i d(t ). ФНЧ модулятора мають АЧХ “корінь зі спектра Найквіста”, вони формують імпульси a _i А (t ) і b_i А (t ). Генератор несійного коливання виробляє cos2pf ₀ t . Фазозсувач на p/2 перетворює це коливання вsin2pf ₀ t . АЧХ “корінь зі спектра Найквіста” записується

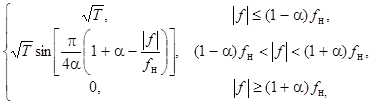= (5.1)

де f _н = 1/(2T ) – частота Найквіста;

a – коефіцієнт закруглення спектра (0 £ a £ 1).

Оскільки ФНЧ збуджується d-функцією, то амплітудний спектр імпульсу A (t ) описується співвідношенням (5.1). Тому ширина спектра імпульсу A (t ) дорівнює (1 + a)/(2T ). Спектр імпульсу a_i A (t )cos2pf ₀ t – це спектр БМ сигналу, тобто дві бокові смуги частот навколо частоти f ₀ . Ширина спектра цього радіоімпульсу (1 + a)/T . Радіоімпульси a_i A (t )cos2pf ₀ t і b_i A (t )sin2pf ₀ t мають одинакові за формою амплітудні спектри. Тому ширина спектра елементарних сигналів s_i (t ) і модульованого сигналу s (t ) (це вірно за умови, що елементарні сигнали на окремих тактових інтервалах незалежні)

F_s = (1 + a)/T . (5.2)

Смуга пропускання каналу зв’язку визначається смугою частот модульованого сигналу

F _к = (1 + a)/T . (5.3)

У каналі зв’язку діє адитивний білий гауссовий шум n (t ) зі спектральною густиною потужності N ₀ /2, –¥ < f < ¥.

У демодуляторі сигнал з каналу зв’язку

a_i A (t ) cos2pf ₀ t + b_i A (t ) sin2pf ₀ t + n (t )

поступає на два підканали. В підканалах включені синхронні детектори, де вхідний сигнал помножується на опорні коливання cos2pf ₀ t та sin2pf ₀ t . Слід врахувати, що

cos² 2pf ₀ t = 0,5 + 0,5 cos2p2f ₀ t , sin² 2pf ₀ t = 0,5 – 0,5 cos2p2f ₀ t , cos2pf ₀ t ×sin2pf ₀ t = 0,5 sin2p2f ₀ t .

Після помножувачів включені ФНЧ, які пропускають низькочастотні складові та ослаблюють складові з частотами біля 2f ₀ . Тому на рис. 3 в на виходах помножувачів показані лише ті складові, які пройдуть через ФНЧ: a_i A (t ) + N_c (t ) та b_i A (t ) + N_s (t ), де N_c (t ) та N_s (t ) – обвідні косинусної та синусної складових шуму на вході демодулятора.

Основне призначення ФНЧ демодулятора – забезпечити максимальне перевищення корисного сигналу над шумом у відліковий момент часу. Виходячи з цієї умови, приходимо до висновку, що ФНЧ повинен бути узгодженим з сигналом A (t ) – його АЧХ повинна співпадати з амплітудним спектром A (t ). Оскільки амплітудний спектр A (t ) описується функцією – співвідношення (5.1), то і АЧХ ФНЧ демодулятора повинна описуватись залежністю . Після проходження імпульсу A (t ) через ФНЧ отримаємо імпульс P (t ) зі спектром Найквіста:

N (f ) = 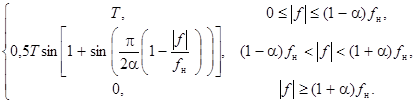(5.4)

Функцію P (t) можна отримати як зворотне перетворення Фур’є від N (f )

P (t ) = . (5.5)

Ключі (Kл) на рис. 3в беруть відліки в момент максимального значення імпульсів P (t ) в підканалах демодулятора. Взяття відліків повторюється через тактовий інтервал Т . Для того, щоб не було міжсимвольної інтерференції, імпульси на виходах ФНЧ демодулятора повинні задовольняти умові відліковості. Завдяки тому, що в цій точці схеми має місце спектр Найквіста, задовольняється умова відліковості.

Після ключів в підканалах демодулятора мають місце оцінки координат переданого сигналу = a_i + x_c та = b_i + x_s , де x_c та x_s – значення завад в момент взяття відліків. Вирішуючий пристрій повинен визначити, якому з М можливих сигналів слід віднести координати (, ). Після винесення рішення про номер сигналу декодер маніпуляційного коду видає n біт, що відповідають цьому номеру у відповідності до табл. 2.

Розділ 4 курсової роботи повинен містити розраховані графіки АЧХ ФНЧ H (f ) = та відгуку ФНЧ демодулятора P (t ) з використанням числових масштабів на осях координат. Слід зробити висновки відносно відсутності міжсимвольної інтерференції. Необхідно порівняти ширину смуги модульованого сигналу F_s з шириною смуги неперервного сигналу F _max , що передається, та зробити відповідний висновок.

6 Аналіз проходження завади через блоки демодулятора

До входу демодулятора поступає завада n (t ) – адитивний білий гауссовий шум із спектральною густиною потужності (СГП) N ₀ /2, –¥ < f <¥. Дію помножувача на заваду можна визначити, враховуючи властивість перетворення Фур’є: помноження на гармонічне коливання частоти f ₀ породжує дві складові, спектри яких зсунуті на +f ₀ i –f ₀ відносно спектру вхідного сигналу. У цьому разі СГП кожної із двох складових отримує множник ¼. Якщо гармонічне коливання має амплітуду , то множник дорівнює ¼×()² = ½. Кожна із складових також є білим шумом, а самі складові незалежні на будь-якій з частот. Тому СГП їх суми удвічі більша за СГП кожної з них, і, таким чином, на виходах кожного з помножувачів має місце білий шум з СГП N ₀ /2, –¥ < f <¥.