Реферат: Аналіз перетворень сігналів

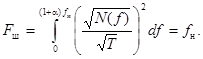(6.1)

З виходу ФНЧ береться відлік завади і маємо x – випадкову величину з гауссовим розподілом ймовірності. Її дисперсія (потужність) дорівнює дисперсії завади на виході ФНЧ

(6.2)

Отже, на основі аналізу проходження сигналу і завади через блоки демодулятора на вході вирішуючого пристрою маємо та де а_і , b_i – числа, що описують переданий сигнал; x_с , x_s – незалежні відліки завади в підканалах демодулятора з середньоквадратичним відхиленням (СКВ) .

Алгоритм роботи вирішуючого пристрою побудований на такому підході. Вся площина, на якій нанесене сигнальне сузір’я, розбивається на М областей, що не пересікаються. Межами областей повинні бути сукупності точок, що знаходяться на рівних відстанях від найближчих точок – це мінімізує ймовірність помилки при винесенні рішення про номер переданого сигналу.

Знання сигнального сузір’я та СКВ завади достатньо для розрахунку ймовірності помилки сигналу. На рис. 2 у кожному сузір’ї позначений сигнал s ₀ . Для сигналів ФМ-4,
АФМ-8 та КАМ-16 помилка сигналу буде мати місце, якщо хоча б одна з координат попаде в область іншого сигналу. Тому умовою виникнення помилки є x > d /2, а ймовірність помилки

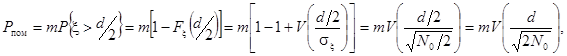(6.3)

де m – кількість помилкових переходів: для ФМ-4 та АФМ-8 m = 2, для КАМ-16 m = 4;

F _x (·) – функція розподілу ймовірності випадкової величини x;

V(·) – інтеграл ймовірності;

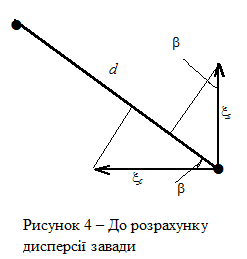
У разі ФМ-8 умова виникнення помилки дещо інша (рис. 4): помилка виникне, якщо сума проекцій x_с та x_s на лінію, що з’єднує найближчі сигнальні точки, перевищить d /2. Сума проекцій x = x_s ×сos b + x_s ×sin b теж має гауссовий розподіл ймовірностей. Оскільки x_с і x_s незалежні, то

(6.4)

Як бачимо, умова виникнення помилки та ж сама: x > d /2, і у разі ФМ-8

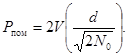(6.5)

Щоб виконати розрахунки ймовірності помилки сигналу, необхідно врахувати зв’язок між d та Е _б , що наведений в табл. 1. Енергія на біт визначається

Е _б = T _б ×P_s , (6.6)

де T _б – тривалість біта, знайдена в завданні 2;

P_s – середня потужність модульованого сигналу, задана в завданні на КР.

Досить d подати через Е _б , а значення N ₀ задане в завданні на КР, і можна розрахувати Р _пом .

Якщо використовується маніпуляційний код Грея, то у разі помилки сигналу виникає помилка лише в одному розряді комбінації, що передається цим сигналом. У такому разі ймовірність помилки двійкового символу (біта) визначається

р = Р _пом /n , (6.7)

де n визначається співвідношенням (4.7).

ВИСНОВКИ ДО КУРСОВОЇ РОБОТИ

Викласти стисло перелік виконаних розрахунків. Зазначити, чи відповідають виконані розрахунки вихідним даним і завданню на КР, а якщо ні, то які розрахунки і чому не відповідають завданню.

ПЕРЕЛІК ПОСИЛАНЬ

1. Теория передачи сигналов : Учебник для вузов / А. Г. Зюко и др. – М.: Радио и связь, 1986.

2. Панфилов И. П., Дырда В. Е. . Теория электрической связи: Учебник для техникумов. – М.: Радио и связь, 1991.

3. Гоноровский И. С . Радиотехнические цепи и сигналы. Учебник для вузов. – М.: Радио и связь, 1986.

4. Баскаков С.И. Радиотехнические цепи и сигналы. Учебник для ВУЗов. – М.: Высшая школа, 1988.

5. Банкет В.Л. Эффективные системы передачи дискретных сообщений: Учебное пособие. – Одесса: ОЭИС, 1982.