Реферат: Анализ случайных процессов в линейных системах радиоэлектронных следящих систем

При увеличении уменьшается, в то время как в первом примере увеличивается.

Эквивалентная шумовая полоса следящих систем

Под эквивалентной шумовой полосой следящей системы понимают полосу пропускания эквивалентной системы, имеющей прямоугольную АЧХ, одинаковое с исходной системой ее значение на нулевой частоте и одинаковую дисперсию на выходе при воздействии на входы систем белого шума (рис.4).

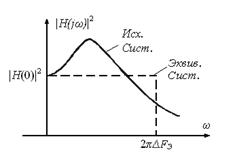
Рис.4. АЧХ исходной и эквивалентной систем.

Чтобы определить полосу пропускания используем условие равенства дисперсий:

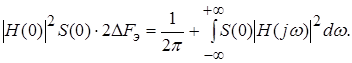
Отсюда

.

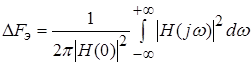Использование значения эквивалентной шумовой полосы позволяет упростить вычисление дисперсии:

; .

Если , то , или ,

где ─ односторонняя спектральная плотность.

Формулы для расчета эквивалентной шумовой полосы систем приведены в табл.1

Таблица 1. Формулы для расчета эквивалентной шумовой полосы.

Оптимизация параметров следящих систем

Для решения задачи оптимизации необходимо определить структуру системы, предъявляемые требования и ограничения, накладываемые на систему, описать воздействия и возмущения, выбрать критерий оптимизации и метод.

Оптимизируем параметры kи2 и T1 в системе (рис.5), в которой задающее воздействие λ(t) – детерминированная функция, а возмущение ─ случайный процесс ξ(t).

В качестве критерия оптимизации используем критерий минимума среднего квадрата ошибки:

; (5)

где - квадрат математического ожидания ошибки слежения.

Рис.5. Структурная схема оптимизируемой системы.

Исходные данные:

; .

Необходимо определить и по критерию (5).

Величина математического ожидания (динамической ошибки) определяется выражением

.

Величина дисперсии ошибки: