Реферат: Аппроксимация непрерывных функций многочленами

и представляют систему линейных уравнений, для нахождения коэффициентов .

Детерминант этой системы, т.е.

,

носит название детерминанта Грама системы векторов g₁ ,g₂ ...g_n .

Так как пространствоН строго нормировано, а векторы g_i линейно независимы, то при любом векторе x система (2) имеет одно и только одно решение. Отсюда вытекает, что детерминант Грама линейно независимых векторов всегда отличен от нуля.

Найдём ещё выражение для квадрата погрешности, с которой вектор y аппроксимирует вектор x, т.е. для величины .

В силу (1), имеем равенство

или

.

Присоединяя это уравнение к системе (2) и исключая , найдём, что

, откуда .

Итак, мы нашли: (3)

Из этого соотношения, и из того, что G(g₁ )=(g₁ ,g₁ )>0 вытекает, что детерминант Грама всегда больше либо равен нулю, причём он обращается в нуль тогда и только тогда, если между векторами есть линейная зависимость (в частности, если один из векторов равен нулю).

1.3. Первая теорема Вейерштрасса.

Мы рассмотрели теорему аппроксимации в произвольном линейном нормированным пространстве Е. Теперь рассмотрим пример линейного нормированного пространства- пространство С.

Пространство С: совокупность всех непрерывных функций x=x(P) от точки Р в ограниченном замкнутом множестве обычного пространства любого числа измерений- это есть линейное нормированное пространство.

Из теоремы в применении к пространству вытекает следующий факт: пусть f(x)- непрерывная функция в конечном интервале [a,b]; тогда при любом n существует полином , который среди полиномов n-й степени наименее уклоняется от f(x), в том смысле, что , где Q_n (x)- произвольный полином n-й степени. Ясно, что .

Теперь докажем, что при . Это утверждение и составляет содержание теоремы Вейерштрасса (1885), которая гласит:

если f(x) непрерывна в конечном замкнутом интервале [a,b], то всякому можно сопоставить полином P_n (x) степени n=n( ), для которого во всём интервале [a,b] имеет место неравенство .

Не нарушая общности, примем, что а=0, b=1. Приведём доказательство С.П.Бернштейна.

Для этого построим полином , и докажем, что равномерно во всём интервале [0,1] . Напишем тождества:

(1); ;

, из которых последите два получаются дифференцированием по р соотношения:

. Из написанных тождеств вытекает, что (2).

Умножая (1) на f(x) и отнимая B_n (x), получим, что

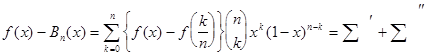, где суммирование в распространено на те значения к, для которых , а суммирование в - на остальные значения к.

Так как f(x) непрерывна в замкнутом интервале [0,1], и, значит, ограничена: во всём этом интервале, то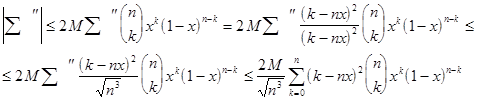

А это выражение на основании (2): , с другой стороны,, где 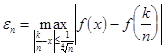, и, значит, при .

Окончательно: , что и доказывает теорему Вейерштрасса.

Заметим, что если P_n (x) равномерно стремится к f(x) при , то f(x) разлагается в равномерно сходящийся ряд.