Реферат: Аппроксимация непрерывных функций многочленами
3.Рассмотрим функцию f(x)=ex .
, 
...
, 
...
, 
4.Рассмотрим функцию f(x)=(a+x)n , 
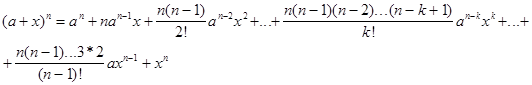
Эту формулу называют биномом Ньютона. Отметим частные случаи:
n=2 (a+x)2 =a2 +2ax+x2
n=3 (a+x)3 =a3 +3a2 x+3ax2 +x3
Приближение функций sinx, cosx, ex алгебраическими многочленами.
В формуле Тейлора для sinx положим n=2m-1
Остаточный член этой формулы имеет вид:
Оценим его модуль. Поскольку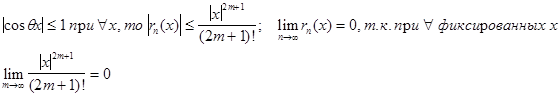 
Отбрасывая остаточный член, получим приближённо:
. Она может быть применена для вычисления значений функции f(x)=sinx при заданных значениях аргумента х. Эти вычисления сводятся к вычислениям значений алгебраического многочлена степени 2m-1
. Следовательно, вместо функции f(x)=sinx можно рассматривать алгебраический многочлен, который приближённо заменяет её. Говорят, что указанный многочлен приближает данную функцию. Оценка такого приближения определяется формулой: 
Полагая n=2m в формуле для cosx, аналогично: 
, погрешность 
.
Например, для приближённой формулы 
В случае функции f(x)=ex , получаем: 
В общем случае, отбросив остаточный член, получим приближённую формулу:
. Она позволяет заменить данную функцию алгебраическим многочленом n-й степени:
Ряд Тейлора.
Обратимся к формуле (1). Разность между функцией f(x) и её многочленом в правой части называют отклонением, которое выражается остаточным членом rn (x).Если в формуле рассматривать всё больше и больше членов, то может оказаться, что отклонение стремится к нулю, но не для всякой функции и не для любого значения х. Однако существует широкий класс функций, для которых остаточный член действительно стремится к нулю при