Реферат: Большое каноническое распределение Гиббса

которая является термодинамическим потенциалом для переменных состояния ().

Такое представление имеет преимущественно общетеоретический интерес, поскольку на его основе четко просматриваются основные постулаты и ограничения. На основе которых осуществляется построение статистической механики.

2) Система в термостате, - состояние задается параметрами (). Функция распределения W_n задается каноническим распределением Гиббса:

Статистическая сумма

связана с макроскопическим параметром – свободной энергией

,

являющейся термодинамическим потенциалом в переменных ().

3) Система, выделенная с помощью воображаемых стенок. Выбранный способ описания очень удобен и широко используется, особенно в статистической механике классических систем. В этом случае фиксированными оказываются параметры (), а число частиц N оказывается микроскопическим параметром. В этом случае функция распределения вводится с помощью большого канонического распределения Гиббса:

Для выбранного способа описания связь с макроскопическими характеристиками системы осуществляется посредством большой статистической суммы:

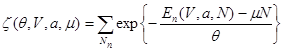
Соответствующим термодинамическим потенциалом является потенциал :

,

который и является термодинамическим потенциалом для системы с воображаемыми стенками.

Этот способ описания также широко используется. Наиболее удобным оказалось использование этого способа в квантовой статистической механике. Относительное неудобство большого канонического формализма связано с часто возникающей необходимостью пересчета результатов к более удобным параметрам ().

4) Система под поршнем. В этом случае фиксируются параметры (), а объем V рассматривается в качестве микроскопического параметра. Тогда функция распределения , задающая структуру смешанного состояния, имеет вид:

Здесь - “гибсовская” статистическая сумма, равная:

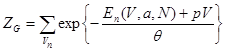
и связанная с термодинамическим потенциалом Гиббса:

,

характеризующим систему, заданную в переменных ().

Этот подход также оказывается удобным при рассмотрении некоторых частных задач.

В случае необходимости состояние термодинамической системы может быть описано и с помощью другого набора параметров. Тогда необходимо ввести соответствующие функции распределения и статистические суммы, связав последние с соответствующим термодинамическим потенциалом. Выбор конкретного способа описания не влияет на окончательный результат, однако способен существенно упростить или усложнить процесс исследования термодинамической системы. Это относится как к точным, так и к приближенным методам.