Реферат: Численные методы линейной алгебры
Расчетные формулы для решения системы (7)
xn = yn ;
![]() (i = n - 1, n - 2, …, 1).
(i = n - 1, n - 2, …, 1).
3. Метод прогонки
Метод прогонки представляет собой простой и эффективный алгоритм решения систем линейных алгебраических уравнений с трехдиагональными матрицами коэффициентов следующего вида
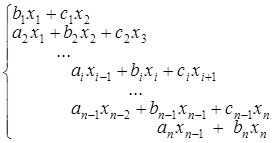
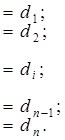 (8)
(8)
Системы такого вида часто возникают при решении различных инженерных задач, например, при интерполяции функций сплайнами.
Преобразуем первое уравнение системы (8) к виду x1 = a1 x2 + b1 , где
a1 = -с1 / b1 и b1 = -d1 / b1 . Подставим полученное для x1 выражение во второе уравнение системы (8)
a2 (a1 x2 + b1 ) + b2 x2 + c2 x3 = d2 .
Представим это уравнение в виде x2 = a2 x3 + b2 , где a2 = -с2 / (b2 + a2 a1 ) иb2 = (d2 - a2 b1 ) / (b2 + a2 a1 ). Полученное для x2 выражение подставим в третье уравнение системы (8) и т.д.
На i-м шаге (1 < i < n) процесса i-е уравнение системы принимает вид
xi = ai xi+1 + bi , (9)
гдеai = -сi / (bi + ai ai-1 ) иbi = (di - ai bi-1 ) / (bi + ai ai-1 ).
На последнем n-м шаге подстановка в последнее уравнение системы (8) выражения xn -1 = an -1 xn + bn -1 дает уравнение an (an -1 xn + bn -1 ) + bn xn = dn , из которого можно определить значение xn = bn = (dn – an bn-1 ) / (bn + an an-1 ).
Значения остальных неизвестных xi (i = n-1, n-2, ..., 1) легко вычисляются по формуле (9).
Таким образом, алгоритм прогонки, подобно методу Гаусса, включает два этапа – прямой ход (прямая прогонка) и обратный ход (обратная прогонка).
Прямой ход метода прогонки состоит в вычислении прогоночных коэффициентов
ai (i = ![]() ) и bi (i =
) и bi (i = ![]() ).
).
При i = 1 эти коэффициенты вычисляются по формулам:
a1 = -с1 / g1 ; b1 = -d1 / g1 ; g1 = b1 .
Для i = ![]() используются следующие рекуррентные формулы:
используются следующие рекуррентные формулы:
ai = -сi / gi ; bi = (di - ai bi-1 ) / gi ; gi = bi + ai ai-1 .
Прямая прогонка завершается при i = n:
bn = (dn – an bn-1 ) / gn ; gn = bn + an an-1 .
Обратный ход метода прогонки позволяет вычислить значения неизвестных. Сначала полагают xn = bn . Затем в обратном порядке по формуле (9) определяют значения неизвестных xn -1 , xn -2 , ..., x1 .
Свойства метода прогонки. Трудоемкость метода прогонки оценивается примерно как 8n арифметических операций, что существенно меньше метода Гаусса. Существование решения системы (8) и его единственность гарантируются при выполнении достаточных условий, задаваемых следующей теоремой.
Теорема [2]. Пусть коэффициенты системы (8) удовлетворяют следующим неравенствам
ïbk ï³ïak ï+ïck ï; ïbk ï>ïak ï; k = ![]() , где a1 = 0; bn = 0. Тогда gi ¹ 0 и ïai ï£
, где a1 = 0; bn = 0. Тогда gi ¹ 0 и ïai ï£