Реферат: Численные методы линейной алгебры

Заметим, что при всех g_i ¹ 0 вычисления по формулам прямой прогонки могут быть доведены до конца (ни один из знаменателей не обратится в нуль). Одновременно все коэффициенты a_i , такие, что ïa_i ï£ 1, обеспечивают устойчивость по входным данным этапа обратной прогонки по формуле (9).

4. Вычисление определителей

Идея последовательного исключения переменных, реализованная в методе Гаусса, может быть использована при вычислении определителей. При этом используются следующие свойства определителей:

1) перестановка двух строк или столбцов определителя не изменяет его абсолютной величины, но меняет знак на противоположный;

2) умножение всех элементов одной строки или одного столбца на любое число равносильно умножению определителя на это число;

3) если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на любой общий множитель, то величина определителя не изменится.

Пусть задан определитель

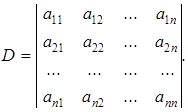
Выберем главный элемент a₁₁ ¹ 0. Если a₁₁ = 0, то выполним перестановку двух строк или столбцов этого определителя, чтобы получить a₁₁ ¹ 0.

Вынесем главный элемент a₁₁ из первой строки за знак определителя

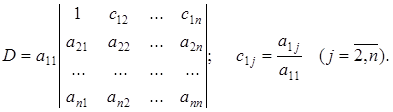
Используя процедуру прямого хода метода Гаусса, преобразуем полученный определитель таким образом, чтобы в первом столбце под единицей были бы все нули. При этом величина определителя не изменится.

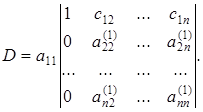
Разложим полученный определитель по элементам первого столбца, что даст понижение его порядка определителя на единицу

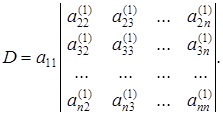
Повторим указанную процедуру (n - 1) раз и окончательно получим

Если при вычислении определителя производилась перестановка строк или столбцов (для выбора главного элемента), то

где s – количество выполненных перестановок.

Таким образом, вычисление определителя detA некоторой матрицы A сводится к выполнению прямого хода метода Гаусса. Абсолютная величина этого определителя равна произведению главных элементов , k = , используемых на каждом шаге прямого хода. Знак определителя зависит от числа перестановок строк и столбцов, выполненных при выборе главных элементов.

Если такие перестановки не производились, то величина определителя также может быть вычислена как произведение диагональных элементов матрицы L, формируемой в процессе LU-разложения исходной матрицы А

5. Вычисление обратных матриц

Обратную матрицу А^-1 имеет любая квадратная матрица А, для которой detA ¹ 0. Пусть дана матрица А = [a_ij ]_{n ´ n} . Для вычисления элементов обратной матрицы используется соотношение

A A^-1 = A^-1 A= E,

где E – единичная матрица.

Обозначим обратную матрицу A^-1 = X = [x_ij ]_{n ´ n} . Тогда получим

A X= E.

Будем рассматривать столбцы матрицы X как векторы