Реферат: Численные методы линейной алгебры

Аналогично выделим столбцы единичной матрицы E

…;

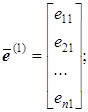
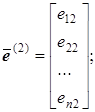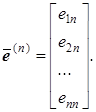
Тогда система линейных уравнений вида

A =

позволяет определить элементы k-го столбца обратной матрицы X = A^-1 . Всего потребуется решить n таких систем с одинаковой матрицей A, но разными правыми частями для k = . Это можно сделать с использованием LU-разложения матрицы коэффициентов A, либо непосредственно с помощью метода Гаусса.

6. Итерационные методы

При решении систем уравнений высокого порядка с разреженными матрицами коэффициентов, которые характерны для большинства задач автоматизации проектирования сложных систем, наиболее эффективно применение итерационных методов. Такие методы (например, последовательных приближений и Зейделя) позволяют получать значения корней системы с заданной точностью в виде последовательности

некоторых векторов, сходящихся к точному решению X*. Эффективность применения итерационных методов зависит от удачного выбора начального приближения и скорости сходимости процесса вычислений.

Итерационные методы используют особенности разреженных матриц коэффициентов, поскольку ненулевые элементы вычисляются по специальным выражениям по мере необходимости. Поэтому для их реализации требуется меньшее количество вычислительных операций (около n² ) и соответствующих затрат машинного времени. Важным преимуществом итерационных методов также является несущественное влияние погрешностей вычислений, так как любое ошибочное приближение может рассматриваться как новый начальный вектор.

Метод последовательных приближений Якоби. Пусть дана система линейных уравнений (1), для которой диагональные элементы

.

Тогда переменную x₁ можно выразить через первое уравнение, - через второе уравнение и т. д.

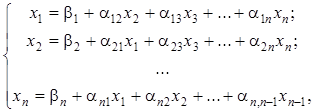(10)

где и

Система (10) называется системой линейных уравнений, приведенной к нормальному виду. Матричная форма записи такой системы представляется как

(11)

где

При решении системы (11) за нулевое приближение корней может быть принят столбец свободных членов, т.е. . Любое k-е приближение ( вычисляется по формуле

Если последовательность приближений ,,, ..., , ... имеет предел , то этот предел является точным решением системы уравнений (2). Итерационная формула, которая может использоваться при программировании метода Якоби, представляется в обозначениях исходной системы (1) следующим образом

Вычисления продолжаются до тех пор, пока значения не станут достаточно близкими к для всех Формальное условие прекращения итерационного процесса записывается как

(12)

где e - некоторое заданное положительное число, характеризующее точность (погрешность) определения корней системы уравнений.

Итерационный метод Зейделя. Метод Зейделя представляет собой модификацию метода последовательных приближений. При определении значения переменной на некоторой (k+1)-й итерации используются уже вычисленные (k+1)-е приближения неизвестных , , ..., , а также значения полученные на предыдущей k-й итерации.

Пусть дана линейная система уравнений (10). Выбранные начальные приближения корней подставляются в первое уравнение