Реферат: Численные методы вычисления интегралов

Пусть промежуток интегрирования разбит на равных частей и для этого разбиения по формуле трапеции получено значение . Значение - совпадает со значением вычисляемого интеграла, если интегрируемая функция линейна, т.е. является многочленом первой степени. По формуле:

(20)

называемой формулой Ромберга , построим - схему:

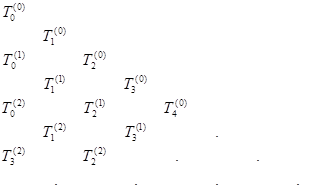(21)

Оказывается, что для интегрируемых по Риману функций, все столбцы и строки - схемы сходятся к исходному значению интеграла.

Пример : Выписать явные формулы для фрагмента - схемы:

Решение :

Пусть Тогда

3. Квадратурные формулы Гаусса

Во всех приведенных до сих пор формулах численного интегрирования Ньютона-Котеса и во всех формулах, получаемых методом Ромберга, используются равноотстоящие узлы. В случае квадратурных формул Гаусса это уже не так. Иначе говоря, смысл квадратурных формул Гаусса состоит в том, чтобы при наименьшем возможном числе узлов точно интегрировать многочлены наивысшей возможной степени. Можно показать, что при гауссовых узлах по полученной формуле можно точно интегрировать многочлены степени .

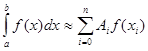(22)

Для количества узлов и соответствующих значений и - составлены таблицы, которые позволяют вычислять интегралы по формуле (22).

Для понимания сути этих таблиц рассмотрим пример.

Пример:

Пусть нам нужно составить квадратурную формулу с двумя узлами ,по которой точно интегрируются многочлены до степень включительно.

Решение: Искомая формула имеет вид:

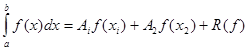,(23)

где - остаток, который обращается в нуль, для