Реферат: Численные методы вычисления интегралов

Тогда, подставляя в (23) имеем:

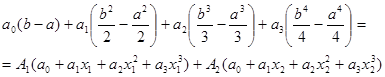(24)

Отсюда, приравнивая коэффициенты при , справа и слева, получаем систему уравнений:

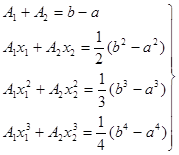(25)

Ее решение имеет вид:

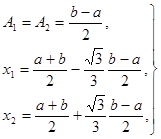(26)

Следовательно, искомая квадратурная формула такова :

.(27)

Ясно, что если нам нужно вычислить интеграл со многими узловыми точками, действуем следующим образом:

а) промежуток интегрирования делим на - равных промежутков и на каждом маленьком промежутке применяем формулу Гаусса с неравноотстоящими узлами (27);

б) полученные результаты складываем.

В случае, когда , оказывается, что узловыми точками при делении отрезка на - частей являются корни соответствующих многочленов Лежандра.

Для вычисления кратных интегралов, их сводят обычно к повторным интегралам, а далее применяют те же самые кубатурные формулы для каждого значения узловых точек, что и в одномерном случае. Однако, надо иметь в виду, что кратные интегралы значительно сложнее вычислять с заданной точностью.

Точность произведённых вычислений зависит от точности аппроксимации подынтегральной функции многочленами.

4. Оценка интегралов

При численном интегрировании наряду с приближёнными формулами представляет также интерес нахождение нижних и верхних границ интегралов. Рассмотрим два метода оценки интегралов:

а) оценка интеграла в случае, когда подинтегральная функция , удовлетворяет условию:

для (28)

б) общий случай.

Рассмотрим интеграл:

(29)

где , . Не умоляя общность, будем считать, что , , тогда (Рис. 1) ясно, что

К Е

N

М

0

Рис. 1

0