Реферат: Дискретные системы радиоавтоматики
(7)
Применим к левой и правой частям уравнения (7) теорему обращения. С учетом теоремы запаздывания оригинала можно записать
![]() , (8)
, (8)
где ![]() ;
;
![]() .
.
Из уравнения (8) можно определить значения оригинала в тактовых точках:
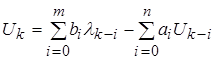 . (9)
. (9)
Уравнение (9) является разностным уравнением, определяющим связь между входной и выходной величинами в тактовых точках.
Операторный коэффициент передачи дискретной системы
Для составления операторного коэффициента передачи вводится оператор запаздывания – с.
Действие его на временную функцию приводит ее к сдвигу по времени на величину Т:
![]() ;
;
![]() ;
;
…………………………
![]() .
.
При использовании оператора с разностное уравнение записывается в виде
![]() ,
,
где
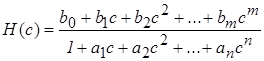 .
.
Чтобы перейти от дискретной ПФ к операторному коэффициенту передачи, необходимо сделать замену:
![]() .
.
Комплексный коэффициент передачи дискретной системы
Комплексный коэффициент передачи дискретной системы (частотную передаточную функцию) можно получить из передаточной функции дискретной системы путем замены ![]() :
:
 .
.
Комплексный коэффициент передачи дискретной системы определяется как отношение комплексных амплитуд управляемой величины Y(kT) и задающего воздействия в тактовых точках kT. По формированию значений выходного процесса в тактовых точках дискретная система эквивалентна непрерывной с комплексным коэффициентом передачи Hд(jw).
Комплексный коэффициент передачи является периодической функцией переменной ![]() с периодом изменения, равным
с периодом изменения, равным
![]() .
.
Устойчивость дискретных систем
Устойчивость дискретной системы связана с расположением полюсов ее передаточной функции на комплексной плоскости. Если все полюса расположены в левой полуплоскости, система устойчива. Таким образом, заменив в передаточной функции H(z) z на esT и решив характеристическое уравнение, можно определить устойчивость.