Реферат: Дискретные цепи

W_x =x² (nT), (2.15)

соответственно в частотной области, согласно равенству Парсеваля,

W_x =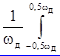X² (w)dw =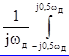X(jw)X^* (jw)d(jw), (2.16)

где X(jw) = X(w)e^{j j ( w )} - спектр сигнала x(nT),

X^* (jw) = X(w)e^{-j j ( w )} - спектр x(-nT) в соответствии с теоремой о спектре инверсного сигнала,

X² (w) = X(jw)ЧX^* (jw) = S_x (jw) - энергетический спектр сигнала x(nT).

На рис.(2.8) показан в качестве примера сигнал x(nT) и его инверсная копия x(-nT) для некоторого частного случая

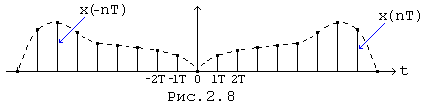
Энергетический спектр выражает среднюю мощность сигнала x(nT), приходящуюся на узкую полосу частот в окрестности переменной w.

Во временной области энергетическому спектру соответствует свертка инверных сигналов, что определяет корреляционную функцию S_x (nT) сигнала x(nT).

. (2.17)

Согласно (2.17) и (2.15) корреляционная функция в точке n = 0 равна энергии сигнала, т. е.

(2.18)

Для периодических дискретных сигналов корреляционная функция и энергетический спектр связаны формулами ДПФ

. (2.19)

Отсюда получаются расчётные формулы энергии периодических дискретных последовательностей

, (2.20)

что соответствует равенству Парсеваля для дискретных периодических сигналов. Корреляционная функция таких сигналов определяется по формуле круговой свёртки

.

Расчет энергии дискретного сигнала можно выполнить при необходимости, применяя равенство Парсеваля относительно Z - изображений сигнала и его инверсной копии (теорема энергий)

, (2.21)

где - Z - изображение корреляционной функции.

Уместно заметить, что применительно к случайным сигналам корреляционная функция чаще определяется формулой с весовым множителем , т.е.

,

соответственно для энергетического спектра

,

что приводит к результату, при котором среднее значение случайной величины с ростом N сходится к постоянной величине.

Свертка сигнала с инверсной копией другого сигнала называется взаимной корреляцией этих сигналов.

Расчёт энергии сигнала в дискретной цепи.

В любой точке дискретной цепи энергию сигнала можно вычислить по известному сигналу или по корреляционной функции сигнала в этой точке. Корреляционную функцию сигнала в некоторой точке цепи можно определить не только по известному сигналу, но и по известной корреляционной функции входного сигнала и импульсной реакции