Реферат: Дисперсийный анализ
Гипотеза H0 отвергается, если фактически вычисленное значение статистики F =S![]() /S
/S![]() больше критического Fα :K1 :K2 , определенного на уровне значимости α при числе степеней свободы k1 =m-1 и k2 =mn-m, и принимается, если F < Fα:K1 :K2 .
больше критического Fα :K1 :K2 , определенного на уровне значимости α при числе степеней свободы k1 =m-1 и k2 =mn-m, и принимается, если F < Fα:K1 :K2 .
F- распределение Фишера (для x > 0) имеет следующую функцию плотности (для ![]() = 1, 2, ...;
= 1, 2, ...; ![]() = 1, 2, ...):
= 1, 2, ...):
![]()
где ![]() - степени свободы;
- степени свободы;
Г - гамма-функция.
Применительно к данной задаче опровержение гипотезы H0 означает наличие существенных различий в качестве изделий различных партий на рассматриваемом уровне значимости.
Для вычисления сумм квадратов Q1 , Q2 , Qчасто бывает удобно использовать следующие формулы:
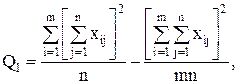 (12)
(12)
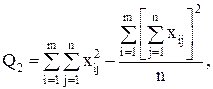 (13)
(13)
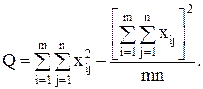 (14)
(14)
т.е. сами средние, вообще говоря, находить не обязательно.
Таким образом, процедура однофакторного дисперсионного анализа состоит в проверке гипотезы H0 о том, что имеется одна группа однородных экспериментальных данных против альтернативы о том, что таких групп больше, чем одна. Под однородностью понимается одинаковость средних значений и дисперсий в любом подмножестве данных. При этом дисперсии могут быть как известны, так и неизвестны заранее. Если имеются основания полагать, что известная или неизвестная дисперсия измерений одинакова по всей совокупности данных, то задача однофакторного дисперсионного анализа сводится к исследованию значимости различия средних в группах данных [1].
1.3 Многофакторный дисперсионный анализ
Следует сразу же отметить, что принципиальной разницы между многофакторным и однофакторным дисперсионным анализом нет. Многофакторный анализ не меняет общую логику дисперсионного анализа, а лишь несколько усложняет ее, поскольку, кроме учета влияния на зависимую переменную каждого из факторов по отдельности, следует оценивать и их совместное действие. Таким образом, то новое, что вносит в анализ данных многофакторный дисперсионный анализ, касается в основном возможности оценить межфакторное взаимодействие. Тем не менее, по-прежнему остается возможность оценивать влияние каждого фактора в отдельности. В этом смысле процедура многофакторного дисперсионного анализа (в варианте ее компьютерного использования) несомненно более экономична, поскольку всего за один запуск решает сразу две задачи: оценивается влияние каждого из факторов и их взаимодействие [3].
Общая схема двухфакторного эксперимента, данные которого обрабатываются дисперсионным анализом имеет вид:
 |
Рисунок 1.1 – Схема двухфакторного эксперимента
Данные, подвергаемые многофакторному дисперсионному анализу, часто обозначают в соответствии с количеством факторов и их уровней.
Предположив, что в рассматриваемой задаче о качестве различных m партий изделия изготавливались на разных t станках и требуется выяснить, имеются ли существенные различия в качестве изделий по каждому фактору:
А - партия изделий;
B - станок.
В результате получается переход к задаче двухфакторного дисперсионного анализа.
Все данные представлены в таблице 1.2, в которой по строкам - уровни Ai фактора А, по столбцам — уровни Bj фактора В, а в соответствующих ячейках, таблицы находятся значения показателя качества изделий xijk (i=1,2,...,m; j=1,2,...,l; k=1,2,...,n).
Таблица 1.2 – Показатели качества изделий
| B1 | B2 | … | Bj | … | Bl | |
| A1 | x11l ,…,x11k | x12l ,…,x12k | … | x1jl ,…,x1jk | … | x1ll ,…,x1lk |
| A2 | x2 1l ,…,x2 1k | x22l ,…,x22k | … | x2jl ,…,x2jk | … | x2ll ,…,x2lk |
| … | … | … | … | … | … | … |
| Ai | xi1l ,…,xi1k | xi2l ,…,xi2k | … | xijl ,…,xijk | … | xjll ,…,xjlk |
| … | … | … | … | … | … | … |
| Am | xm1l ,…,xm1k | xm2l ,…,xm2k | … | xmjl ,…,xmjk | … | xmll ,…,xmlk |
Двухфакторная дисперсионная модель имеет вид:
xijk =μ+Fi +Gj +Iij +εijk , (15)
где xijk - значение наблюдения в ячейке ij с номером k;
μ - общая средняя;
Fi - эффект, обусловленный влиянием i-го уровня фактора А;
Gj - эффект, обусловленный влиянием j-го уровня фактора В;
Iij - эффект, обусловленный взаимодействием двух факторов, т.е. отклонение от средней по наблюдениям в ячейке ij от суммы первых трех слагаемых в модели (15);
εijk - возмущение, обусловленное вариацией переменной внутри отдельной ячейки.