Реферат: Дисперсийный анализ

Групповые средние находятся по формулам:

- в ячейке:

,

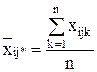по строке:

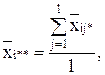
по столбцу:

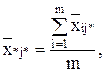
общая средняя:

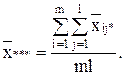
В таблице 1.3 представлен общий вид вычисления значений, с помощью дисперсионного анализа.

Таблица 1.3 – Базовая таблица дисперсионного анализа

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Средние квадраты
Межгрупповая (фактор А)		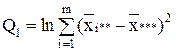m-1
Межгрупповая (фактор B)		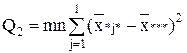l-1
Взаимодействие		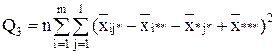(m-1)(l-1)
Остаточная		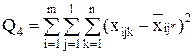mln - ml
Общая		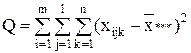mln - 1

Проверка нулевых гипотез H_A , H_B , H_AB об отсутствии влияния на рассматриваемую переменную факторов А, B и их взаимодействия AB осуществляется сравнением отношений , , (для модели I с фиксированными уровнями факторов) или отношений , , (для случайной модели II) с соответствующими табличными значениями F – критерия Фишера – Снедекора. Для смешанной модели III проверка гипотез относительно факторов с фиксированными уровнями производится также как и в модели II, а факторов со случайными уровнями – как в модели I.

Если n=1, т.е. при одном наблюдении в ячейке, то не все нулевые гипотезы могут быть проверены так как выпадает компонента Q₃ из общей суммы квадратов отклонений, а с ней и средний квадрат , так как в этом случае не может быть речи о взаимодействии факторов.

С точки зрения техники вычислений для нахождения сумм квадратов Q₁ , Q₂ , Q₃ , Q₄ , Q целесообразнее ис­пользовать формулы:

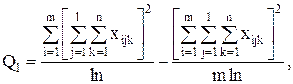
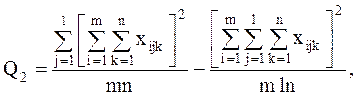
Q₃ = Q – Q₁ – Q₂ – Q₄ .

Отклонение от основных предпосылок дисперсионного ана­лиза — нормальности распределения исследуемой переменной и равенства дисперсий в ячейках (если оно не чрезмерное) — не сказывается существенно на результатах дисперсионного анализа при равном числе наблюдений в ячейках, но может быть очень чувствительно при неравном их числе. Кроме того, при нерав­ном числе наблюдений в ячейках резко возрастает сложность аппарата дисперсионного анализа. Поэтому рекомендуется пла­нировать схему с равным числом наблюдений в ячейках, а если встречаются недостающие данные, то возмещать их средними значениями других наблюдений в ячейках. При этом, однако, искусственно введенные недостающие данные не следует учиты­вать при подсчете числа степеней свободы [1].

Заключение

Современные приложения дисперсионного анализа охватывают широкий круг задач экономики, биологии и техники и трактуются обычно в терминах статистической теории выявления систематических различий между результатами непосредственных измерений, выполненных при тех или иных меняющихся условиях.

Благодаря автоматизации дисперсионного анализа исследователь может проводить различные статистические исследования с применение ЭВМ, затрачивая при этом меньше времени и усилий на расчеты данных. В настоящее время существует множество пакетов прикладных программ, в которых реализован аппарат дисперсионного анализа. Наиболее распространенными являются такие программные продукты как:

- MSExcel;

- Statistica;

- Stadia;

- SPSS.

В современных статистических программных продуктах реализованы большинство статистических методов. С развитием алгоритмических языков программирования стало возможным создавать дополнительные блоки по обработке статистических данных.

Дисперсионный анализ является мощным совре­менным статистическим методом обработки и анализа экс­периментальных данных в психологии, биологии, медици­не и других науках. Он очень тесно связан с конкретной ме­тодологией планирования и проведения экспериментальных исследований.

Дисперсионный анализ применяется во всех областях научных исследований, где необходимо проанализировать влияние различных факторов на исследуемую переменную.

Список используемых источников

1. Кремер Н.Ш. Теория вероятности и математическая статистика. М.: Юнити – Дана, 2002.-343с.

2. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2003.-523с.

3. Гусев А.Н. Дисперсионный анализ в экспериментальной психологии. – М.: Учебно-методический коллектор «Психология», 2000.-136с.

4. http://www.statsoft.ru/home/textbook/modules/stanman.html

5. Шеффе Г. Дисперсионный.анализ М., Наука: 1980, 512 стр.

6. http://www.ucheba.ru/referats/8214.html