Реферат: Движение в центрально-симметричном поле

Из формулы (2,8) ( для ) видно, что допускаемое решение уравнения Шредингера ( вблизи точки, где ) расходится при не быстрее чем . Если поле обращается при в бесконечность медленнее чем , то в уравнении Шредингера в области вблизи начала координат можно вовсе пренебречь по сравнению с остальными членами, и мы получим те же решения, что и для свободного движения, т.е. . Наконец, если поле обращается в бесконечность быстрее чем ( как с ), то волновая функция вблизи начала координат пропорциональна . Во всех этих случаях произведение обращается при в нуль.

Далее, исследуем свойства решений уравнения Шредингера в поле, спадающем на больших расстояниях по закону при произвольном его виде на малых расстояниях. Предположим сначала, что . Легко видеть, что в этом случае может существовать лишь конечное число отрицательных уровней энергии[1] . Действительно, при энергии уравнение Шредингера на больших расстояниях имеет вид (2,1) с общим решением (2,4). Но функция (2,4)не имеет ( при ) нулей; поэтому все нули искомой радиальной волновой функции лежат на конечных расстояниях от начала координат и их число, во всяком случае, конечно. Другими словами, порядковый номер уровня , замыкающего дискретный спектр, конечен.

Если же , то дискретный спектр содержит бесконечное число отрицательных уровней энергии. Действительно, волновая функция состояния имеет на больших расстояниях вид (2,9) с бесконечным числом нулей, так что ее порядковый номер во всяком случае бесконечен.

Наконец, пусть поле во всем пространстве. Тогда при происходит падение частицы. Если же , то отрицательные уровни энергии отсутствуют вовсе. Действительно, волновая функция состояния будет во всем пространстве вида (2,7); она не имеет вовсе нулей на конечных расстояниях, т.е. соответствует наиболее низкому (при данном ) уровню энергии.

3. Движение в кулоновом поле ( сферические координаты ).

Очень важным случаем движения в центрально-симметричном поле является движение в кулоновом поле

( - положительная постоянная ). Мы будем рассматривать сначала кулоново притяжение, соответственно чему будем писать . Из общих соображений заранее очевидно, что спектр отрицательных собственных значений энергии будет дискретным ( с бесконечным числом уровней ), а спектр положительных энергий – непрерывным.

Уравнение (1,8) для радиальных функций имеет вид

(3,1)

Если речь идет об относительном движении двух притягивающихся частиц, то под надо подразумевать их приведенную массу.

В вычислениях, связанных с кулоновским полем, удобно пользоваться вместо обычных особыми единицами для измерения всех величин, которые мы будем называть кулоновскими единицами. Именно, в качестве единиц измерения массы, длины и времени выберем соответственно

Все остальные единицы выводятся отсюда; так, единицей энергии будет

.

Далее будем пользоваться этими единицами.

Уравнение (3,1) в новых единицах принимает вид

(3,2)

Дискретный спектр.

Введем вместо параметра и переменной новые величины:

(3,3)

При отрицательных энергиях есть вещественное положительное число. Уравнение (3,2) после подстановки (3,3) приобретает вид

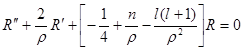(3,4)

( штрихи обозначают дифференцирование по ).

При малых решение, удовлетворяющее необходимым условиям конечности, пропорционально ( см. (1,15)). Для выяснения асимптотического поведения при больших опускаем в (3,4) члены с и и получаем уравнение

откуда . Интересующее нас исчезающее на бесконечности решение, следовательно, при больших ведет себя, как .

Виду этого естественно сделать подстановку

, (3,5)