Реферат: Двоично-ортогональные системы базисных функций

, (4)

где спектр Уолша

. (5)

Для проверки правильности расчета спектральных коэффициентов может быть использовано равенство Парсеваля

.

Если ограничиться N членами в разложении, то получим усеченный ряд Уолша:

,(6)

гдеt Î [0,T]; N=T/ D t; t = a D t приt ® ¥ a ® ¥ , a - сдвигпооси;

wal(n,Q) после преобразования аргументов.

Для практических расчетов можно использовать формулу:

.

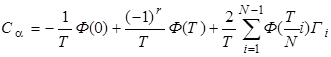где: ; (7)

r - ранг спектрального коэффициента с номером a (число двоичных разрядов числа a в которых имеются 1).

i - номер подынтервала определения функции x(t) ;

. (8)

Приэтом Г_i принимает значение ±1 или 0 в зависимости от того меняет ли W _a (i/N) в точке i/N знак с "+" на "-",c "-" на " +" или знак не меняется.

Пример 1. Разложить функцию x(t) = at в ряд по упорядоченным по Пэли функциям Уолша при N=8, T=1, a=1.

Решение: Определим Ф(t):

.

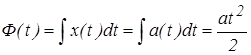Определим спектральные коэффициенты с учетом функций Уолша упорядоченным по Пэли по формуле (7)

C₀ = aT/2;

C₁ = -aT/2 + 0 +0 + 0 +2(aT/4) + 0 + 0 + 0 = -aT/4;

C₂ = -aT/2 + 0 + 4aT/64) + 0 - 16aT/64 + 0 +36aT/64 +0 =-aT/8;

C₃ = aT/2 + 0 + 4aT/64) + 0 + 0 + 0 - 36aT/64 +0 = 0;

C₄ =-aT/2 + aT/64 - 4aT/64 + 9aT/64 - 16aT/64 + 25aT/64 –

- 36aT/64 + 49aT/64 =-aT/16;

C₅ =C₆ =C₇ =0.

Ряд Уолша - Пэли имеет вид:

.
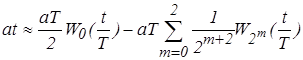