Реферат: Двоично-ортогональные системы базисных функций

X

1

0 1 t

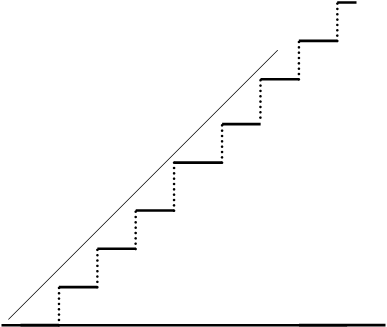
Рис . 3. Аппроксимация функции x(t)=at рядом Уолша – Пэли

4. Дискретное преобразование Уолша

Дискретное преобразование Уолша (ДПУ) производится при использовании дискретных функций Уолша W _a (i/N) Þ Wal(n, Q) и выполняется над решетчатыми сигналами x(i) , при этом число отсчетов N должно быть двоично -рациональным, т. е. N = 2ⁿ , где n = 1, 2,... , i - определяет номер точки дискретного интервала определения a = 0, 1,..., N-1 .

Формулы дискретного ряда Уолша имеют вид:

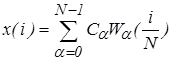,(9)

где дискретный спектр Уолша

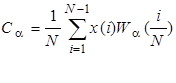. (10)

Для проверки правильности расчета спектральных коэффициентов может быть использовано равенство Парсеваля:

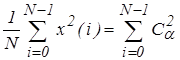(11)

График дискретной функции Уолша, упорядоченных по Пели приведен на рис.

W₀

012 3 4 5 6 7i

W₁

W₂

W₃

W₄

W₅

W₆

W₇

Рис. 4 График дискретной функции Уолша

Для ускорения дискретных преобразований Уолша используются алгоритмы быстрого преобразования Уолша (БПУ) аналогичного БПФ.

БПУ также производится прореживанием по времени и частоте.

Применение преобразований Уолша. Преобразования Уолша находят широкое применение при:

- построении цифровых фильтров;

- исследовании систем автоматического управления (моделировании, оптимизации, идентификации и т. д.);