Реферат: Эконометрика 10

2) определение коэффициентов регрессии (этап идентификации).

Предположим, на этапе спецификации установлено, что между величинами x и y существует линейная зависимость. Реальные значения y будут отличаться от этой теоретической зависимости.

В общем случае линейное уравнение связи двух переменных, учитывающее случайные отклонения, можно представить в виде:

y = + x + ,

(6.1)

где – отклонение от теоретически предполагаемого значения;

и - неизвестные параметры (коэффициенты регрессии).

В уравнении (6.1) можно выделить две части:

 систематическую, = + x, где характеризует некоторое среднее значение y для данного значения x ;

 случайную ().

Коэффициенты и описывают вид зависимости для генеральной совокупности. Так как при выполнении подобных исследований всегда имеют дело с выборочной совокупностью, то истинные значения параметров и являются неизвестными, и мы можем говорить лишь об их оценках. Обозначим эти оценки, соответственно, а и b , тогда уравнение регрессии с оцененными параметрами будет иметь вид:

i = a + bxi ,

(6.2)

где n - объем выборки.

Обозначим через e_i отклонение реального значения отклика y_i от теоретически рассчитанного по уравнению _i .

Параметры a и b уравнения регрессии чаще всего оцениваются с помощью метода наименьших квадратов (МНК) .

Суть его состоит в том, чтобы зная положение точек на плоскости XY, так провести линию регрессии, чтобы сумма квадратов отклонений этих точек от проведенной прямой вдоль оси OY была минимальной.

Математически критерий оценки параметров линейной парной регрессии записывается так:

Q = = = → min.

Условие существования экстремума функции – равенство нулю производной:

= - 2 (yi - a - bxi ) = 0, = - 2 (yi - a - bxi )xi = 0.

Раскрыв скобки и выполнив преобразования, получим систему из двух уравнений с двумя неизвестными:

na + bxi = yi , axi + b = xi yi .

Разделив первое уравнение на n , получим:

a + b = ,

т.е. метод наименьших квадратов дает прямую, проходящую через точку (, ).

Решая систему, получим расчетные формулы для нахождения коэффициентов уравнения регрессии:

a = - b.

(6.3)

Заметим, что данные значения могут быть легко получены средствами пакета Microsoft Excel . Для вычисления коэффициента a используется функция ОТРЕЗОК, коэффициента b – функция НАКЛОН.

3. Коэффициент линейной корреляции

Величина влияния фактора на исследуемый отклик может быть оценена при помощи коэффициента линейной парной корреляции , характеризующего тесноту (силу) линейной связи между двумя переменными.

Коэффициент можно определить по формуле:

.

(6.4)
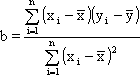
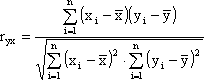