Реферат: Эконометрика 10

5. Сравнение коэффициентов регрессии

Допустим, в результате анализа получено следующее уравнение регрессии:

y = 2,4 + 0,8x1 + 3,2x2 .

Если величины x₁ и x₂ являются соизмеримыми, то мы можем сопоставить влияние факторов x₁ и x₂ путем непосредственного сравнения соответствующих коэффициентов. В нашем примере можно сказать, что фактор x₂ воздействует на y в четыре раза сильнее.

В тех случаях, когда x₁ и x₂ измеряются в разных величинах для сравнения степени их влияния прибегают к нормированию коэффициентов регрессии и определяют так называемый бета-коэффициент ():

j = aj ∙ ,

(6.7)

где a_j - соответствующий коэффициент уравнения регрессии;

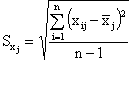, - среднеквадратическое отклонение значений переменной x_j (m – число учитываемых факторов);

- среднеквадратическое отклонение значений переменной y .

Математически бета-коэффициент показывает, на какую часть величины среднеквадратического отклонения меняется среднее значение зависимой переменной с изменением независимой переменной на одно среднеквадратическое отклонение при фиксированном на постоянном уровне значении остальных независимых переменных.

Заметим, что некоторые авторы именуют бета-коэффициент стандартизированным коэффициентом регрессии .

Для целей сравнения коэффициентов регрессии (сравнения силы влияния каждого фактора на отклик) также может быть использован коэффициент эластичности (Э):

Эj = aj ∙ .

(6.8)

Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении соответствующего фактора на один процент.

6. Коэффициент множественной корреляции

Экономические явления чаще всего адекватно описываются именно многофакторными моделями. Поэтому возникает необходимость обобщить рассмотренное выше корреляционное отношение (6.4) на случай нескольких переменных.

Теснота линейной взаимосвязи между переменной y и рядом переменных x_j , рассматриваемых в целом, может быть определена с помощью коэффициента множественной корреляции .

Предположим, что переменная y испытывает влияние двух переменных - x и z . В этом случае коэффициент множественной корреляции может быть определен по формуле:

.

(6.9)

где r_yx , r_yz , r_xz - простые коэффициенты линейной парной корреляции, определенные из соотношения (6.4).

Коэффициент множественной корреляции заключен в пределах 0 ≤ R ≤ 1. Он не меньше, чем абсолютная величина любого парного или частного коэффициента корреляции с таким же первичным индексом.

С помощью множественного коэффициента (по мере приближения R к 1) делается вывод о тесноте взаимосвязи, но не о ее направлении. Величина R² , называемая множественным коэффициентом детерминации , показывает, какую долю вариации исследуемой переменной (y ) объясняет вариация остальных учтенных переменных (x , z ).

7. Коэффициент частной корреляции

Иногда представляет интерес измерение частных зависимостей (между y и x_j ) при условии, что воздействие других факторов, принимаемых во внимание, устранено. В качестве соответствующих измерителей приняты коэффициенты частной корреляции .

Рассмотрим порядок расчета коэффициента частной корреляции для случая, когда во взаимосвязи находятся три случайные переменные – x , y , z . Для них могут быть получены простые коэффициенты линейной парной корреляции – r_yx , r_yz , r_xz . Однако большая величина этого коэффициента может быть обусловлена не только тем, что y и x действительно связаны между собой, но и в силу того, что обе переменные испытывают сильное действие третьего фактора – z .

Коэффициент частной корреляции отличается от простого коэффициента линейной парной корреляции тем, что он измеряет парную корреляцию соответствующих признаков (y и x ) при условии, что влияние на них третьего фактора (z ) устранено.

Соответствующая расчетная формула:

.

(6.10)

Частный коэффициент корреляции, так же как и парный коэффициент корреляции r (рассчитанный по формуле (6.4)), может принимать значения от -1 до 1.

8. Оценка параметров нелинейной регрессии