Реферат: Экзаменационные билеты по численным методам за первый семестр 2001 года

примерный перечень экзаменационных вопросов

ЧИСЛЕННЫЕ МЕТОДЫ

1. Математическая модель и ее погрешности.
2. Представление чисел в ЭВМ. Работа компьютера с плавающей или фиксированной точкой.
3. Виды погрешности: неустранимая, численного метода, вычислительная, абсолютная, относительная.
4. Значение цифры числа. Верная значащая цифра числа.
5. Вычисление абсолютной и относительной погрешностей суммы (разности) двух чисел, если известны погрешности каждого числа.
6. Определение абсолютной и относительной погрешностей произведения двух чисел, если известны погрешности каждого числа.
7. Определение абсолютной и относительной погрешностей при делении двух чисел, если известны погрешности каждого числа.
8. Устойчивые и неустойчивые задачи по исходным величинам.
9. Корректно поставленная задача.
10. Системы линейных уравнений. Их математическая запись. Расширенная матрица. Геометрический смысл умножения матрицы на вектор. Эквивалентные преобразования.
11. Прямые и итерационные методы решения системных уравнений.
12. Какую матрицу называют диагональной, единичной, верхней или нижней треугольной, симметричной, ленточной, трехдиагональной?
13. Какую матрицу называют хранимой, воспроизводимой?
14. Опишите метод Гаусса решения систем линейных уравнений.
15. Представление исходной матрицы системы уравнений в виде произведения двух треугольных матриц. Модификация метода Гаусса.
16. Обусловленность систем линейных уравнений.
17. Итерационный метод решения систем линейных уравнений. Выбор начального приближения.
18. Приведение системы к виду, удобному для итераций.
19. Метод простой итерации.
20. Метод Зейделя.
21. Сформулируйте достаточные условия сходимости методов простой итерации и Зейделя.
22. В чем заключается метод верхней релаксации для ускорения сходимости итерационных методов?
23. Определение обратной матрицы А^-1 к матрице А и определителя матрицы А численным методом.
24. Собственные значения и собственные векторы матрицы. Их геометрический смысл. Собственные значения симметричной матрицы.
25. Что называется характеристическим многочленом матрицы?
26. Чем отличается полная проблема собственных значений от частичной проблемы собственных значений?
27. Какая существует связь между собственными значениями матрицы A и обратной ей матрицы A^-1 ?
28. Как степенным методом определить наименьшее собственное значение матрицы A?
29. В чем заключается степенной метод нахождения максимального собственного значения матрицы A и соответствующего ему собственного вектора?
30. От чего зависит скорость сходимости степенного метода нахождения максимального собственного значения матрицы A?
31. Особенности решения нелинейных задач на примере одного уравнения.
32. В чем заключается отделение корней нелинейного уравнения F(x) = 0?
33. Что называется порядком сходимости итерационного метода решения одного нелинейного уравнения?
34. Что называется погрешностью приближенного значения x_k для корня x_* нелинейного уравнения?
35. Как оценить погрешность приближенного решения x_k для нахождения корня нелинейного уравнения F(x) = 0, если известно минимальное значение производной F^' (x) на отрезке [a, b]?
36. Что называется областью притяжения корня для итерационного метода решения нелинейного уравнения?
37. Что называется двусторонним приближением для нахождения корня нелинейного уравнения?
38. Какой итерационный процесс называется монотонно сходящимся?
39. Какой итерационный процесс называется колеблющимся для нахождения корня нелинейного уравнения? В чем его достоинство?
40. При каких условиях сходится метод половинного деления для нахождения корня уравнения F(x) = 0?
41. Перечислите достоинства и недостатки метода половинного деления для решения нелинейного уравнения F(x) = 0.
42. В чем заключается метод простой итерации для решения нелинейного уравнения F(x) = 0?
43. Сформулируйте достаточное условие сходимости метода простой итерации.
44. Какой порядок сходимости имеет метод простой итерации? Приведите соответствующее неравенство.
45. Сформулируйте принцип сжатых отображений для функции одной переменной.
46. Метод Ньютона для решения нелинейного уравнения. Его геометрическая интерпретация. Достаточное условие сходимости.
47. Приведите неравенство, связывающее погрешности на двух последовательных итерациях метода Ньютона нахождения корня нелинейного уравнения. Каков порядок сходимости этого метода?
48. Приведите условия Фурье для функции F(x) при решении нелинейного уравнения F(x) = 0. Где они используются?
49. В чем заключается метод секущих для решения нелинейного уравнения F(x) = 0?
50. В чем заключается комбинированный метод хорд и касательных для нахождения корня нелинейного уравнения F(x) = 0?
51. Приведите расчетные формулы метода простой итерации для решения системы нелинейных уравнений.
52. Приведите какое-либо достаточное условие сходимости метода простой итерации для решения системы нелинейных уравнений.

53. В чем заключается метод Ньютона решения системы нелинейных уравнений?

1. Аппроксимация функций. В каких случаях она необходима?
2. Точечная и непрерывная аппроксимации.
3. Многочисленное приближение и его преимущество.
4. Тригонометрические многочлены.
5. Интерполирование функции. Интерполяционный многочлен.
6. В чем заключается критерий близости двух функций f(x) и φ (x) при среднеквадратичном приближении?
7. Что называется сплайн-интерполяцией?
8. Что называется наилучшим равномерным приближением функции f(x) на отрезке [ a , b ]?
9. В чем заключается линейная интерполяция?
10. В чем заключается различие локальной и глобальной интерполяции?
11. Приведите общий вид интерполяционного многочлена Лагранжа.
12. Что называется разностной схемой при численном решении обыкновенного дифференциального уравнения методом конечных разностей?
13. В чем заключается квадратичная интерполяция?
14. Первые и вторые разности таблично заданной функции с постоянным шагом аргумента.
15. Выведите формулу линейной интерполяции, взяв первые два члена интерполяционного многочлена Ньютона.
16. Чему равна погрешность интерполяционного многочлена Лагранжа?
17. В чем заключается явление Рунге при многочленной интерполяции с равномерно расположенными узлами?
18. В чем заключается различие степенных разложений Тейлора от степенных разложений Чебышева?
19. Как вычисляются многочлены Чебышева с помощью рекурентных соотношений?
20. Почему многочлен Чебышева называется наименее уклоняющимся от нуля?
21. В чем отличие ошибок, получаемых при среднеквадратичном и чебышевском равномерном приближении?
22. Какой вид имеет квадратурная формула прямоугольников для вычисления определенного интеграла?
23. Что называется численным интегрированием при вычислении определенного интеграла?
24. В каких случаях для вычисления определенного интеграла приходится использовать формулы численного интегрирования?
25. Что называется квадратурной формулой для приближенного вычисления определенного интеграла?
26. Что называется составной квадратурной формулой?
27. Напишите квадратурную формулу метода прямоугольников для вычисления определенного интеграла.
28. Напишите составную квадратурную формулу метода прямоугольников для вычисления определенного интеграла.
29. Какую погрешность имеют квадратурные формулы метода прямоугольников при вычислении определенного интеграла?
30. Приведите квадратурную формулу метода трапеций для вычисления определенного интеграла.
31. Приведите составную квадратурную формулу метода трапеций для вычисления определенного интеграла.
32. Какую погрешность имеют квадратурные формулы метода трапеций при вычислении определенного интеграла?
33. Приведите квадратурную формулу метода Симпсона для вычисления определенного интеграла.
34. Приведите составную квадратурную формулу метода Симпсона для вычисления определенного интеграла.
35. Какую погрешность имеют квадратурные формулы метода Симпсона при вычислении определенного интеграла?
36. Что называют квадратурными формулами Ньютона – Котеса?
37. В чем заключается главная идея метода Гаусса для задачи численного интегрирования?
38. В чем заключается метод Рунге повышения точности численного интегрирования?
39. Как получить уточнение по методу Рунге при использовании метода Симпсона для вычисления определенного интеграла?
40. Что называют адаптивными алгоритмами при решении задачи численного интегрирования?
41. Приведите конечно-разностные выражения для первой производной.
42. Что понимается под термином численное дифференцирование?
43. Что называется порядком погрешности аппроксимации производной? Приведите примеры погрешности разных порядков.
44. Приведите конечно-разностное выражение для второй производной, использующее центральную разность.
45. Приведите конечно-разностное выражение для первой производной в граничной точке со вторым порядком точности.
46. Как использовать правило Рунге для получения уточненного значения производной?
47. В чем заключается метод конечных разностей решения обыкновенных дифференциальных уравнений?
48. Дать определение первых и вторых конечных разностей для таблично заданной функции.
49. Какие уравнения называются разностными? Что называется порядком разностных уравнений?
50. Приведите примеры разностных уравнений первого и второго порядка, в которые входят сеточные функции.
51. Линейное разностное уравнение n-го порядка и его общее решение.
52. Однородные разностные уравнения второго порядка с постоянными коэффициентами и их решение.
53. Что называется задачей Коши для обыкновенного дифференциального уравнения? Приведите пример.
54. Что называется краевой задачей для обыкновенного дифференциального уравнения? Приведите пример.
55. В чем заключается метод конечных разностей для решения обыкновенного дифференциального уравнения?
56. Что называется разностной схемой для решения обыкновенного дифференциального уравнения?
57. Какая разностная схема называется устойчивой?
58. Разностная схема аппроксимирует дифференциальное уравнение и дополнительные условия. Что это означает?
59. В каком случае решение, получаемое по разностной схеме, сходится к решению дифференциальной задачи?
60. Какая разностная схема для решения задачи Коши называется явной?
61. Какой разностный метод решения задачи Коши называется одношаговым?
62. Какой разностный метод решения задачи Коши называется многошаговым?
63. Какой разностный метод решения задачи Коши называется неявным?
64. Опишите метод Эйлера для решения задачи Коши .
65. Какой порядок имеет локальная и глобальная погрешность метода Эйлера?
66. Приведите формулы метода Эйлера с пересчетом для решения задачи Коши .
67. Приведите формулы метода Рунге – Кутта для решения задачи Коши .
68. Что включает в себя полная постановка задачи для уравнений в частных производных?
69. Какие задачи для уравнений в частных производных называются стационарными, а какие – нестационарными? Какие дополнительные условия надо для них задать?
70. Какая задача для уравнений в частных производных называется корректно поставленной?
71. В чем заключается метод сеток для решения уравнений в частных производных?
72. Приведите конечно-разностные формулы для частных производных в произвольной точке (i , j ) сетки с помощью центральных разностей.
73. В чем заключается аппроксимация дифференциальной задачи разностной схемой?
74. Какая разностная схема для уравнений в частных производных называется устойчивой?
75. При каких условиях решение разностных уравнений сходится к решению уравнений с частными производными с соответствующими им дополнительными условиями?
76. Напишите явную разностную схему для уравнения теплопроводности и опишите ее свойства.

типы задач

1. Решите методом Гаусса систему уравнений
.

2. Найдите LU размножение для матрицы А: .

3. Задана система линейных уравнений и , где A из вопроса 136, а ={12, 3, 12}. Используя LU расхождение, полученное в предыдущем вопросе, найти решение системы.

4. Дана система уравнений и ее приближенное решение: x₁ ≈0,7; x₂ ≈0,4. Вычислить вектор невязки уравнения .

5. Задана система линейных уравнений: Привести систему к виду, удобному для итераций, так, чтобы метод Зейделя сходился.

6. Какая из матриц обладает свойством диагонального преобладания: и .

7. Задана линейная система: . Записать ее в виде, удобном для итерации, и сделать один шаг методом Зейделя, положив = = 0.

8. Задана линейная система: . Записать ее в виде, удобном для итерации, и сделать один шаг методом простой итерации, положив = = 0.

9. Задана матрица А=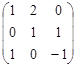 . Найти обратную матрицу А^-1 .

10. Найти определитель матрицы А=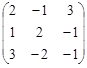 методом Гаусса.

11. Как отделить корни уравнения ?

12. Сделайте один шаг методом половинного деления для нахождения корня уравнения на интервале [0,1].

13. Во сколько раз уменьшится исходный интервал [c, d], если сделать 4 шага методом половинного деления?

14. Как сделать 2 шага методом простой итерации для уравнения х = 0,5 – х³ ? Начальное приближение х₀ = 0.

15. Будет ли сходиться итерационный метод решения уравнения х = 0,5(1 – х³ ) при х₀ = 0 для корня, находящегося на интервале [0, 1]?

16. Дано нелинейное уравнение х³ + 2х – 1 = 0, корень которого находится в интервале [0, 1]. Записать это уравнение в виде, удобном для итерации, чтобы метод итераций сходился.

17. Задано нелинейное уравнение F(x) = sinx + x – 0,1 = 0. Сделать один шаг методом Ньютона, взяв x₀ = 0.

18. Проверить сходимость метода Ньютона для уравнения sinx + x – 0,1 = 0, если x₀ = 0,01.

19. Задана табличная функция
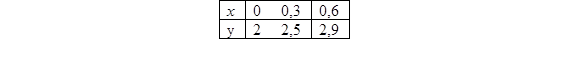C помощью линейной интерполяции найти y(0, 5).

20. Задана табличная функция
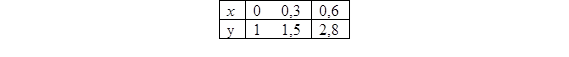C помощью квадратичной интерполяции найти y(0, 2).

21. Подынтегральная функция y = f(x) задана таблицей
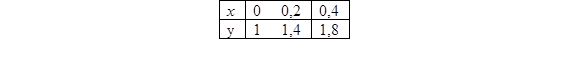Взяв h = 0,4, вычислить методом прямоугольников .

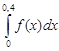22. Подынтегральная функция y = f(x) задана таблицей
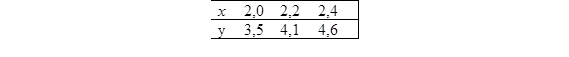Взяв h = 0,2, вычислить интеграл 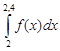на отрезке [2; 2,4] методом трапеций.

23. Подынтегральная функция y = f(x) задана таблицей
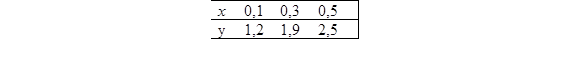Взяв h = 0,2, вычислить интеграл 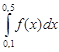на отрезке [0,1; 0,5] методом Симпсона.

24. Подынтегральная функция y = f(x) задана таблицей
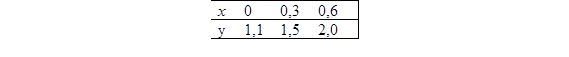Вычислить интеграл 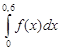методом трапеций с шагом h = 0,3 и h = 0,6 и получить уточненное значение методом Рунге.

25. Задано разностное уравнение , определенное на всей числовой оси и удовлетворяющее условию . Как найти решение этого уравнения?

26. Найти решение разностного уравнения .

--> ЧИТАТЬ ПОЛНОСТЬЮ <--