Реферат: Элементарные частицы и космология
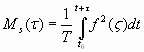 (4)
(4)
заметим, что интеграл
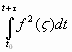 (5)
(5)
выражает энергию чистого сигнала. Тогда выражение (4) запишется как
![]() (6)
(6)
где ![]() - энергия сигнала в промежутке времени измерения. Назовем полученную величину
- энергия сигнала в промежутке времени измерения. Назовем полученную величину ![]() “массой” сигнала, а величину
“массой” сигнала, а величину ![]() - потенциалом.
- потенциалом.
Далее попробуем применить полученные выражение для оценки массы сигнала. В качестве сигнала рассмотрим звуковой сигнал в газе. Для идеального газа существует известная зависимость скорости звука от температуры идеального газа.
![]() (7)
(7)
соответственно
![]() (8)
(8)
Подставив в (6) выражение температуры из (8) запишем
![]() (9)
(9)
или, иначе
![]() (10)
(10)
Всегда можно подобрать систему единиц такую, что произведение kR будет равно единице и выражение примет вид
![]() (11)
(11)
5. Пространство и время
5.1. Время
Пусть ![]() - некоторая функция распределения величин, полностью описывающая состояние системы в данный момент времени. Будем называть ее функцией состояния. Следующее состояние системы будет описано иной функцией. Условимся обозначать состояния системы натуральным числом n, а соседние состояния обозначать соответственно n+1 и n-1. Тогда переход системы из состояния с номером n в состояние n+1 можно записать
- некоторая функция распределения величин, полностью описывающая состояние системы в данный момент времени. Будем называть ее функцией состояния. Следующее состояние системы будет описано иной функцией. Условимся обозначать состояния системы натуральным числом n, а соседние состояния обозначать соответственно n+1 и n-1. Тогда переход системы из состояния с номером n в состояние n+1 можно записать
![]() (12)
(12)
где F - оператор перехода. Тогда
![]() (13)
(13)
где ![]() - дифференциальный оператор перехода.
- дифференциальный оператор перехода.
Для дальнейших рассуждений нам понадобится выяснить, что считать переходом системы из одного состояния в другое.
Переход к уравнению (13) возможен при неизменных условиях преобразования, то есть в применении к системе, при условии неизменности внешнего воздействия. В общем случае ![]() будет зависеть от номера перехода.
будет зависеть от номера перехода.
Как уже было отмечено, переход из одного стационарного состояния в другое должно удовлетворять условию
![]() (14)
(14)
или, исходя из (13)
![]() (15)
(15)
![]() (16)
(16)
Для дальнейших рассуждений необходимо сделать небольшие замечания. Как уже говорилось вначале главы, n - это порядковый номер события. При этом событием будем считать осреднение параметров в системе по всему набору элементов системы, точнее осреднение по сменам их состояний. На самом деле, смысл этого определения выясниться дальше, придется его уточнить и подкорректировать. Пока же будем рассуждать как условились. Теперь мы можем провести предельный переход в уравнении (13)