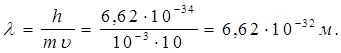Реферат: Елементи квантової фізики
Е = h n ,
Р = h / l . (1.3)
Ліві частини системи (1.3) є ознаками частинок (корпускул), а праві частини (частота і довжина хвилі) є ознаками електромагнітних хвиль. В формулах (1.3) відображено дуалізм (хвиля-частинка) світла. Світло з одного боку схоже на газ, який складається з фотонів з енергією Е і імпульсом Р . З другого боку він є неперервною електромагнітною хвилею з частотою v . В різних експериментальних умовах світло проявляє або корпускулярні, або хвильові властивості.
В 1924 році французький фізик Луї де Бройль висунув гіпотезу, яка незабаром знайшла дослідне підтвердження, згідно якої кількісні співвідношення частинок, такі ж, як і для фотонів. Сміливість гіпотези де Бройля полягає якраз в тому, що співвідношення (1.3) постулюються не лише для фотонів, але і для інших мікрочастинок, які мають масу спокою. Таким чином, будь-якій мікрочастинці, імпульс якої Р= m u , відповідає хвиля з імпульсом P = h / l .
Тому
![]()
![]() ,
, ![]() (1.4)
(1.4)
де m - маса частини; u - швидкість руху частинки.
Формула (1.4) називається формулою де Бройля. Вона дає можливість оцінити довжину хвилі мікроскопічної частинки масою m , яка рухається з швидкістю u . У макроскопічних тіл ці властивості не проявляються. Так, у тіла масою 1 г, яке летить з швидкістю 10 м/с довжина хвилі де Бройля дорівнює
|
|
Жоден прилад не зможе зареєструвати таку коротку хвилю (на сьогодні реєструють довжини порядку 10-18 м).
У мікрочастинок (електрон, протон, нейтрон і ін.) маса співрозмірна з атомною одиницею маси, а тому довжина хвилі де Бройля при невеликих швидкостях може бути досить великою. Так, довжина хвилі електрона з кіне-тичною енергією 1 еВ дорівнює 13,3 . 10-10 м. Із збільшенням швидкості мікрочастинки довжина хвилі де Бройля зменшується, а при дуже великих швидкостях мікрочастинка веде себе як класична частинка.
В 1925 році після ознайомлення з дисертацією де Бройля, де описується корпускулярно-хвильовий дуалізм матерії, Ейнштейн пише Максу Борну так: «Прочитайте її! Хоч і відчувається, що цю дисертацію писав божевільний, але як солідно вона написана». Це говорить про те що в ті часи ідея де Бройля виглядала досить неправдоподібно із-за відсутності дослідного обґрунтування, яке б підтверджувало хвильові властивості елементарних частинок.
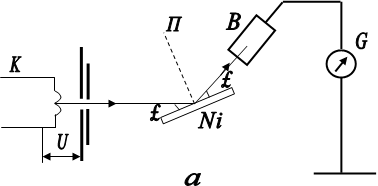
Лише в 1927 році американські фізики Девісон і Джермер виявили, що пучок електронів, який розсіювався від природної дифракційної гратки - монокристал нікелю - дає чітку дифракційну картину. Схема установки зображена на рис.1.1.
 |
Д
Рис. 1. 1
Електронний пучок, який вилітав з нагрітої нитки катода К, прискорювався полем з різницею потенціалів U , і проходячи через ряд діафрагм Д у вигляді досить вузького пучка падав на монокристал нікелю а . Іонізаційна камера В , яка з’єднувалась з гальванометром G , вимірювала величину струму І , пропорційну числу електронів, відбитих від грані монокристала нікелю. Кут a під час досліду залишався сталим.
![]() Дослід полягав в тому, що вимірювався струм І через гальванометр, як функція прискорюваної різниці потенціалів U . В результаті досліду було установлено, що при монотонній зміні прискорюваної різниці потенціалів U , струм гальванометра змінювався не монотонно, а давав ряд максимумів. Графік залежності струму І від величини Ö U показано на рис.2.
Дослід полягав в тому, що вимірювався струм І через гальванометр, як функція прискорюваної різниці потенціалів U . В результаті досліду було установлено, що при монотонній зміні прискорюваної різниці потенціалів U , струм гальванометра змінювався не монотонно, а давав ряд максимумів. Графік залежності струму І від величини Ö U показано на рис.2.
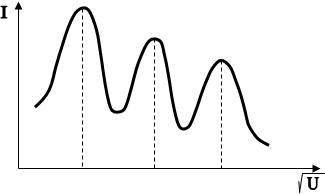 |
Рис. 1.2
Одержана залежність I = f ( ![]() ) характеризується рядом майже однаково віддалених максимумів сили струму. Звідси випливає, що відбивання електронів здійснюється лише при певних різницях потенціалів, тобто при відповідних швидкостях електронів.
) характеризується рядом майже однаково віддалених максимумів сили струму. Звідси випливає, що відбивання електронів здійснюється лише при певних різницях потенціалів, тобто при відповідних швидкостях електронів.
Аналогічне явище спостерігається при відбиванні рентгенівських променів від кристала кварцу. Відбивання у певному напрямі характеризується кутом a згідно закону Вульфа-Брегга
2d sin a = k l , (1.5)
де l - довжина рентгенівської хвилі ; d - стала кристалічної гратки; k - порядок відбивання.
Порівнявши наведені факти, можна зробити висновок, що електронний пучок проявляє хвильові властивості і при цьому довжина хвилі електронного пучка залежить від швидкості електронів.
Дійсно, oскільки d й a в умовах досліду є незмінними, виконання умови (1.5) з хвильової точки зору визначається значенням довжини хвилі l . Числову відповідність результатів розсіювання електронного пучка з умовою (1.5) можна одержати, якщо довжину хвилі електронного пучка l зв’язати з швидкістю u електронів за допомогою формули де Бройля
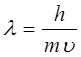 , (1.6)
, (1.6)
де h - стала Планка ; m - маса електрона.
Швидкість електронів u , які пройшли прискорювану різницю потенціалів U знайдемо з умови
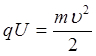 . (1.7)
. (1.7)
Звідки
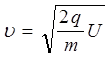 . (1.8)
. (1.8)
Підставивши (1.8) в (1.6), одержимо:
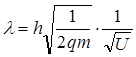 . (1.9)
. (1.9)
Довжину хвилі з (1.9) підставимо в (1.5)
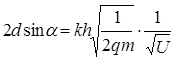 . (1.10)
. (1.10)
Рівність (1.10) визначає ті значення різниці потенціалів U , при яких струм І через гальванометр досягає максимумів.
Так як в умовах досліду кут a є сталим, то для різних максимумів, при певних значеннях k з (1.10) маємо
![]() , (1.11)
, (1.11)