Реферат: Елементи квантової фізики

Хвильове число к може набувати довільних значень, так як вільні частинки в системі можуть мати практично будь-які постійні швидкості. Це говорить про те, що енергетичний спектр вільних частинок є суцільним.

Густина імовірності перебування вільної частинки в довільних точках осі х дорівнює

де - комплексна спряжена хвильова функція. Звідки

Густина імовірності вільної частинки в будь-якій точці осі х є сталою величиною. Невизначеності вільної частинки в координаті в такому випадку дорівнюють безмежності. Цей висновок є добрим підтвердженням співвідношення невизначеностей Гейзенберга.

1.3.2. Частинка в одновимірному потенціальному ящику

Розглянемо приклад просторово-обмеженого одновимірного руху квантової частинки в глибокому потенціальному ящику з вертикальними стінками, шириною l . Потенціальна енергія електрона зовні і всередині такого ящика має наступні значення:

U ( x )=0 при 0 < x < l , (1.37)

U ( x )= ¥ при x £ 0 й x ³ l

Графік залежності потенціальної енергії частинки U ( x ) від х показаний на рис 1.5.

Частинка в такому ящику може вільно рухатись на ділянці 0<х<l . На кінцях цього інтервалу вона стикається з абсолютно твердими стінками. Непрозорість цих стінок визначається необмеженим ростом потенціальної енергії U ( x ) в точках х=0 і х =l .

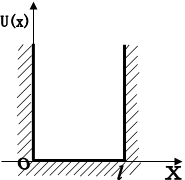Рис. 1.5

Прикладом руху електрона в потенціальному ящику може бути рух колективізованих електронів усередині металу. Як відомо, в класичній електронній теорії вважали, що поза металом потенціальна енергія електрона дорівнює нулю, а всередині металу - вона від’ємна і чисельно дорівнює роботі виходу електрона з металу. Інакше кажучи, вважали, що рух електронів обмежений потенціальним бар’єром прямокутної форми з плоским дном. В нашому випадку потенціальний ящик значно простішої форми ніж реальний випадок електрона в металі.

Так як частинка не виходить за межі ділянки 0 < х < l , то імовірність знайти її за межами цієї ділянки дорівнює нулю. Це означає, що рівняння Шредінгера для стаціонарних станів можна доповнити граничними умовами і

Запишемо рівняння Шредінгера для частинки в потенціальному ящику

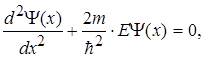(1.38)

де m - маса частинки; - стала Дірака; Е - повна енергія частинки; Y (х) - хвильова функція.

Введемо позначення

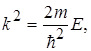(1.39)

де к - хвильове число хвиль де Бройля для електрона, який перебуває усередині потенціального ящика.

Рівняння (1.38) набуде вигляду

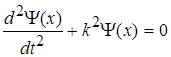(1.40)

Знайдемо розв’язок рівняння (1.40), подібно до аналогічних диференціальних рівнянь гармонічних коливань, в тригонометричній формі

(1.41)

де А,В і С - сталі величині.

З граничних умов одержуємо:

а) Y (0)=0 ; 0=А cosB ^. 0+ CsinB ^. 0

Звідки А=0 ; В ¹ 0 і С ¹ 0 .

б) Y ( l)=0 ; 0=CsinB^. l .

звідки при С ¹ 0, В l = n p , або де n = 1,2,3. .......

Хвильова функція з урахуванням граничних умов набуде вигляду:

(1.42)

Константу С у формулі (1.42) знайдемо із умови нормування

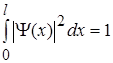(1.43)

або

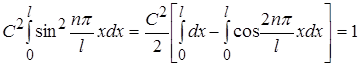. (1.44)

Другий інтеграл у виразі (1.44) при будь-яких значеннях n дорівнює нулю, тому