Реферат: Елементи квантової фізики

Справедливість цього рівняння обгрунтована тим, що всі висновки які випливають із нього, знайшли своє експериментальне підтвердження. Рівняння Шредінгера відіграє в квантовій механіці таку ж роль, як і рівняння Ньютона в класичній.

В загальному випадку рівняння Шредінгера має вигляд

(1.30)

де m - маса частинки ; - потенціальна енергія частинки в силовому полі; - уявна одиниця; - стала Дірка;

- оператор Лапласа.

Із-за присутності в рівнянні Шредінгера (1.30) уявної одиниці хвильова функція , яка задовольняє цьому рівнянню, завжди комплексна. Не кожна функція може бути розв’язком рівняння (1.30). Перш за все ця функція повинна бути скінченою, неперервною і мати неперервні перші похідні. Ці вимоги мають чисто математичний характер. Крім того - хвильова функція повинна бути однозначною , інакше буде порушений її фізичний зміст.

Рівняння Шредінгера за часом є лінійним диференціальним рівнянням 1-го порядку. Із теорії диференціальних рівнянь відомо, що кожне лінійне рівняння в частинних похідних повинно мати безліч розв’язків, причому таких, що всяка лінійна комбінація будь-якої сукупності розв’язків теж буде його розв’язком.

Слід зауважити, що рівняння Шредінгера, подібно до законів Ньютона в класичній механіці, не є результатом якогось теоретичних доведень, а є узагальненням багатьох дослідних фактів, встановлених при вивченні мікросвіту. Відмітимо також, що рівняння Шредінгера описує рух частинок, швидкість яких значно менша швидкості світла, так як співвідношення між кінетичною енергією і імпульсом справедливе лише при цих умовах. В релятивістському випадку для описання хвильових властивостей мікрочастинок слід користуватись іншими рівняннями, наприклад рівняннями Дірака чи Клейна-Гордона.

1.2.3. Рівняння Шредінгера для стаціонарних станів

Потенціальна енергія частинки залежить від координат x , y , z і часу t . Якщо потенціальна енергія U від часу не залежить і відповідно повна енергія також не змінюється з часом, то хвильову функцію можна подати у вигляді добутку двох співмножників

. (1.31)

Перший співмножник в (1.31) залежить лише від часу, а другий - лише від координат ().

Розв’язки рівняння Шредінгера, для яких потенціальна енергія, а також густина імовірностей не змінюються з часом, називаються стаціонарними. Стаціонарні стани не виключають залежності хвильової функції від часу, а лише обмежують її гармонічним законом .

Підставимо хвильову функцію (1.31) в рівняння Шредінгера (1.30)

.

Після скорочення на експоненту, одержуємо:

, (1.32)

де ; Е - повна енергія частинки; - потенціальна енергія частинки , яка є функцією лише координат; - хвильова функція; m - маса частинки; - стала Дірака ().

Стаціонарне рівняння Шредінгера (1.32) є однорідним лінійним диференціальним рівнянням другого порядку відносно координат x , y , z . У випадку, коли =0 , це рівняння не має фізичного змісту. В рівнянні Шредінгера для стаціонарних станів є єдиний вільний параметр - повна енергія частинки Е . При деяких значеннях повної енергії це рівняння може мати нульові розв’язки. Ті значення повної енергії, при яких рівняння (1.32) буде мати нульові розв’язки, називаються власними значеннями. Кожному такому власному значенню енергії відповідає свій розв’язок рівняння (1.32).

Стаціонарне рівняння Шредінгера дає не лише значення хвильової функції, але й значення цієї функції в стаціонарних станах.

1.3. Найпростіші задачі квантової механіки

1.3.1. Рух вільної частинки.

1,3.2. Частинка в одновимірному потенціальному ящику.

1.3.3. Гармонічний квантовий осцилятор.

1.3. 4. Проходження частинки крізь потенціальний бар’єр.

Тунельний ефект.

1.3.1. Рух вільної частинки

Найпростішим рухом квантової частинки є вільний рух. Прикладом такого руху є рух електронів в металах і напівпровідниках. В цьому випадку потенціальна енергія частинок дорівнює нулю. При вільному русі повна енергія частинки збігається з кінетичною, а її швидкість є сталою величиною. Такому рухові в класичній механіці відповідає рівномірний і прямолінійний рух.

Нехай рівномірний рух квантової частинки відбувається в напрямі осі х , яка співпадає з напрямком вектора швидкості. Стаціонарне рівняння Шредінгера для вільної частинки запишеться:

(1.33)

де m - маса частинки; Е - повна енергія частинки.

Рівняння (1.33) є диференціальним рівнянням другого порядку з сталими коефіцієнтами, розв’язком якого може бути функція

(1.34)

де А і к - сталі величини; і - уявна одиниця.

Підстановка (1.34) в (1.33) дасть тотожність

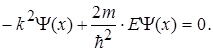
Звідки 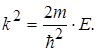(1.35)

В співвідношенні (1.35) к - хвильове число хвиль де Бройля; Е - повна енергія частинки; m - маса частинки.