Реферат: Энергетические характеристики гравитационных и магнитных аномалий

Переходя под интегралом от автокорреляционной функции к энергетическому спектру и меняя пределы интегрирования, для первого интеграла правой части получаем

(1.37)

С другой стороны, для знакопеременных аномалий на основании теорем о спектре производных получим

где S₁ (ω) — спектр аномалии f(x) (например, гравитационной аномалии V_xz или V_zz ), а S(ω) — спектр исходной незнакопеременной аномалии (например, аномалии V_z ), который обращается в нуль только при . При ω = 0 с учетом формула (1.2) из последнего равенства получим.

(1.38)

или

Тогда должно выполняться равенство

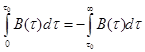, (1.39)

т.е. положительная часть площади под функцией B(τ) и осью τ должна равняться отрицательной. Поэтому из равенства (1.36) получим

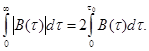(1.40)

Это равенство определяет важное свойство автокорреляционных функций знакопеременных аномалий и позволяет заменить бесконечные пределы интегрирования модуля автокорреляционных функций конечными — только от 0 до τ₀ .

На основании формулы (3.37) запишем аномалии

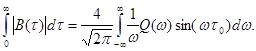(1.41)

Это равенство позволяет перейти от интегрирования автокорреляционных функций к интегрированию энергетических спектров.

Для трехмерных знакопеременных по осям x и y аномалий получим равенство, аналогичное (1.40) (соответственно для произвольных и осесимметричных аномалий):

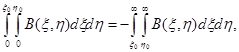(1.42)

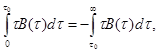(1.43)

где ξ₀ и η₀ — горизонтальные координаты точек перехода автокорреляционной функции через нуль. Тогда аналогично равенству (1.40) сможем написать:

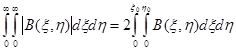(1.44)

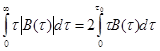(1.45)

Аналогично формуле (1.41) в трехмерном случае соответственно для произвольных f(x, y) осесимметричных f(r) знакопеременных аномалий с учетом равенств (1.42), (1.43) мож­но получить следующие выражения:

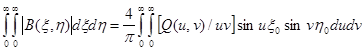(1.46)

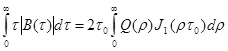(1.47)

Полученные соотношения имеют важное практическое применение, в частности они будут использованы в дальнейшем при определении значений радиуса корреляции знакопеременных гравитационных и магнитных аномалий.

Расчётная часть

Возьмём нормированную автокорреляционную функцию для случаев вертикальной производной порядка n = 0. Рассмотрим ёе поведение для бесконечной материальной горизонтальной линии, бесконечной горизонтальной полосы и для бесконечной вертикальной материальной полосы.

1. Бесконечная горизонтальная материальная линия.