Реферат: Энергетические характеристики гравитационных и магнитных аномалий

1. Введение

2. Теоретическая часть

3. Расчётная часть

4. Список литературы

Введение

В данной работе рассматриваются элементы теории случайных функций и их применение для интерпретации гравитационных и магнитных аномалий. Аппарат теории случайных функций и основанный на нём статистический подход можно применять в различных ситуациях. Во-первых, когда мало известно о параметрах аномалий или геологических объектах, которыми они вызваны. Во-вторых, когда поставленную задачу гравиразведки и магниторазведки можно решить только с применением аппарата теории случайных функций и ,наконец, в-третьих, при решении задач различными детерминированными методами.

Получаемые данные, корреляционные функции и связанные с ними энергетические спектры аномалий имеют следующие свойства: малая чувствительность к погрешностям наблюдений; взаимозаменяемость; чётность получаемых выражений.

В работе также приведены примеры применения теоретического материала к практике. Представлены расчёты для бесконечной горизонтальной материальной линии, бесконечной вертикальной материальной полосы и бесконечной горизонтальной полосы.. Для исследуемых функций построены графики при различных исходных данных.

Теоретическая часть

ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГРАВИТАЦИОННЫХ И МАГНИТНЫХ АНОМАЛИЙ

Энергия процесса f(t), соответствующая изменению времени от t= -t₁ , до t = t₁ определяется интегралом

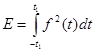
Среднее значение энергии за время 2t₁ (или средняя мощность) определяется выражением

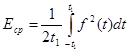
Через эти интегралы прямо можно выразить основные статистические характеристики сигналов — автокорреляционную функцию и энергетический спектр. Поэтому эти характеристики называют еще и энергетическими характеристиками сигналов.

Аналогичные интегралы можно написать и для отрезка профиля при изменении расстояния x от –T до +T, а именно:

,

Эти интегралы выражают площадь между кривой квадрата функции f² (x) и осью x при изменении x от –T до +T и среднюю величину этой площади, т.е. сумму значений квадратов функции и средний квадрат функции.

По аналогии с величинами E и E_ср гравиразведке и магниторазведке значения F и F_ср также называют энергией функции f(x) (энергия и средняя величина энергии). При этом величину f² (x) называют мгновенной энергией, а значение интеграла полной энергией функции f(x) (если, конечно, он существует). Автокорреляционная функция В(τ) и энергетический спектр сигнала Q(ω) однозначно можно выразить через указанные интегралы, определяющие энергии. Поэтому функции B(τ) и Q(ω) также называют энергетическими характеристиками функции f(x), в нашем случае гравитационной или магнитной аномалии.

В следующих разделах рассматриваются энергетические характеристики и детерминированных, и случайных аномалий. Причем первые являются аномалиями f(x) определенной формы из класса (по В. Н. Страхову), для которых существует интеграл .

§ 1. Определение энергетических спектров и корреляционных функций аномалий

Аномалии известной формы (детерминированные сигналы)

Пусть f(x) — некоторая ограниченная вдоль профиля функция строго определенной формы, а S(ω) — ее трансформанта Фурье (предполагаем, что она существует) и пусть далее существует интеграл .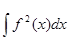

Автокорреляционной функцией такого сигнала f(x) (по определению В.Н. Страхова, если функция f(x) принадлежит классу , h > 0) называется функция

(1.1)

Определив преобразование Фурье такой функции B(τ), получим энергетический спектр (спектральная плотность) сигнала f(х):

(1.2)

Тогда

(1.3)

Между автокорреляционной функцией В(τ) аномалии f(х) и ее энергетическим спектром Q(ω) существует связь, определяемая этой парой преобразований Фурье. Если определим функцию Q(ω) через значения простого спектра S(ω) аномалии f(x), то получим выражение

(1.4)

(это в симметричной форме записи. В несимметричной форме записи коэффициент будет отсутствовать).

--> ЧИТАТЬ ПОЛНОСТЬЮ <--